Классификаторы библиотеки scikit-learn рассматриваются на задаче классификации ирисов Фишера-Андерсона, описание которых дано в виде набора из данных о 150 экземплярах ириса, по 50 экземпляров из трех следующих видов (рис. 1):

Рис. 1. Ирисы
Для каждого экземпляра приведены 4 следующие характеристики (в см.):
Данные находятся в файле iris.csv. (рис. 2):
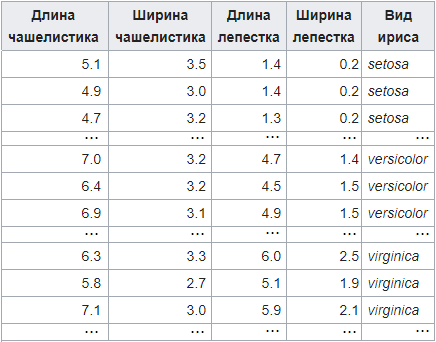
Рис. 2. Примеры записей файла iris.csv
На основании этого набора данных требуется построить правило классификации, определяющее класс растения.
Замечание. Один из классов (Iris setosa) линейно-разделим от двух остальных (рис. 3).
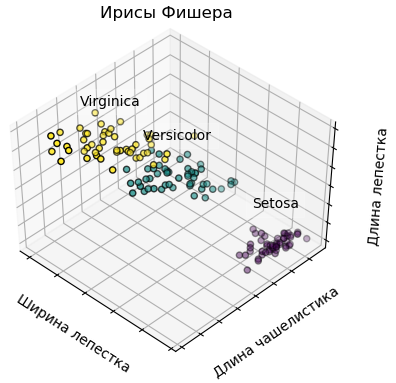
Рис. 3. Представление классов ирисов по трем характеристикам
Рис. 3 будет выведен, если в приводимой далее программе задать groundTruth = True.
Первая строка файла iris.csv содержит заголовки столбцов, далее следуют строки данных:
sepalLength,sepalWidth,petalLength,petalWidth,variety
5.1,3.5,1.4,.2,Setosa
4.9,3,1.4,.2,Setosa
Гистограммы характеристик ирисов, описанных в вышерассмотренном наборе, показаны на рис. .
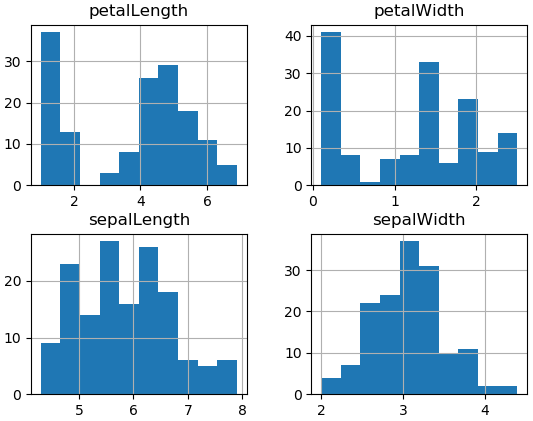
Рис. 4. Гистограммы характеристик ирисов (получены по файлу iris.csv)
Для построения гистограмм можно применить следующий код:
import pandas
import matplotlib.pyplot as plt
iris = pandas.read_csv('iris.csv')
iris.hist()
plt.show()
Используются следующие классификаторы:
import numpy as np
import pandas
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # Для управления 3D-изображением (посредством мышки)
from sklearn.metrics import accuracy_score
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression, SGDClassifier
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.neural_network import MLPClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier
from sklearn.svm import SVC
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
import sys # Для sys.exit()
np.random.seed(348)
# Загрузка данных
iris = pandas.read_csv('iris.csv')
print(iris.shape) # (150, 5)
print(iris.head(10)) ## Печать первых 10 строк данных, загруженных из файла iris.csv
print(iris.describe()) # count, mean, std и др.
print(iris.groupby('variety').size()) # Setosa 50, Versicolor 50, Virginica 50
#
# Ветви программы
hist = False # True - вывод гистограмм
groundTruth = False # True - вывод классов по трем характеристикам: ширина лепестка, длина чашелистика, длина лепестка
cross_val = True # True, False - вывод карт вероятности по двум характеристикам: длина и ширина чашелистика
#
if hist:
## Гистограммы характеристик ирисов
iris.hist()
plt.show()
sys.exit()
if groundTruth:
# Заменяем имена классов на номера
iris["variety"] = iris["variety"].map({"Setosa":0, "Versicolor":1, "Virginica":2})
# Выводим результаты наблюдений (по 3-м характеристикам)
X = iris.values[:, 0:4]
y = iris.values[:, 4]
fig = plt.figure(1, figsize = (5, 4))
ax = Axes3D(fig, rect = [0, 0, .95, 1], elev = 48, azim = 134)
for name, label in [('Setosa', 0), ('Versicolor', 1), ('Virginica', 2)]:
ax.text3D(X[y == label, 3].mean(),
X[y == label, 0].mean(),
X[y == label, 2].mean() + 2, name,
horizontalalignment = 'center',
bbox = dict(alpha = 0.2, edgecolor = 'w', facecolor = 'w'))
ax.scatter(X[:, 3], X[:, 0], X[:, 2], c = y, edgecolor = 'k')
ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([])
ax.set_xlabel('Ширина лепестка')
ax.set_ylabel('Длина чашелистика')
ax.set_zlabel('Длина лепестка')
ax.set_title('Ирисы Фишера')
ax.dist = 12
fig.show()
sys.exit()
iris_array = iris.values
x = iris_array[:, 0:4]
y = iris_array[:, 4]
#
# Используемые методы:
# 1. SGD Classifier (SGD) - Линейный классификатор с SGD-обучением (stochastic gradient descent - стохастический градиентный спуск)
# 2. Support Vector Machines (SVM) - Метод опорных векторов (kernel = 'linear')
# 3. Random Forest Classifier (RF) - Случайный лес (используются деревья решений)
# 4. Gaussian process classification (GP) - Гауссовская классификация (основана на аппроксимации Лапласа)
# 5. AdaBoost (Adaptive Boosting) Classifier (AB) - Адаптивное усиление
# 6. Decision tree classifier (DT) - Дерево решений (http://scikit-learn.org/stable/modules/tree.html)
# 7. Logistic Regression (LR) - Логистическая регрессия
# 8. Gaussian Naive Bayes (NB) - Гауссовский наивный байесовский классификатор
# 9. Support Vector (SV) Classification - Метод опорных векторов http://scikit-learn.org/stable/modules/svm.html#svm-classification
# 10. MLP (Multi-layer Perceptron) Classifier (MLP) - Многослойный перцептрон
# 11. K-Nearest Neighbors (KNN) - Метод K-ближайших соседей
# 12. Quadratic Discriminant Analysis (QDA) - Квадратичный дискриминантный анализ
# 13. Linear Discriminant Analysis (LDA) - Линейный дискриминантный анализ
classifiers = []
if cross_val:
classifiers.append(('SGD', SGDClassifier(max_iter = 1500, tol = 1e-4)))
classifiers.append(('SVL', SVC(kernel = 'linear', C = 0.025, probability = True))) # C - штраф в случае ошибки
classifiers.append(('RF', RandomForestClassifier(max_depth = 5, n_estimators = 10, max_features = 1)))
if cross_val:
classifiers.append(('GP', GaussianProcessClassifier()))
classifiers.append(('AB', AdaBoostClassifier()))
classifiers.append(('DT', DecisionTreeClassifier()))
classifiers.append(('LR', LogisticRegression(solver = 'lbfgs', max_iter = 500, multi_class = 'auto')))
classifiers.append(('NB', GaussianNB()))
classifiers.append(('SVR', SVC(gamma = 2, C = 1.0))) # gamma - коэффициент ядра для 'rbf' - radial basis function, 'poly' and 'sigmoid'
classifiers.append(('MLP', MLPClassifier(alpha = 0.01, max_iter = 200, solver = 'lbfgs', tol = 0.001)))
classifiers.append(('KNN', KNeighborsClassifier(3)))
classifiers.append(('QDA', QuadraticDiscriminantAnalysis()))
classifiers.append(('LDA', LinearDiscriminantAnalysis()))
# Оценка методов
if cross_val:
results = []
names = []
k = 10
for name, classifier in classifiers:
# Генерируем индексы для выделения обучающих и тестовых данных
# k - 1 подвыборок будут использованы для обучения, а одна - для проверки (валидации)
kfold = model_selection.KFold(n_splits = k, random_state = 348)
## cv - стратегия кросс-валидации
cv_results = model_selection.cross_val_score(classifier, x, y, cv = kfold, scoring = 'accuracy')
results.append(cv_results)
names.append(name)
#print("%s: %f (%f)" % (name, cv_results.mean(), cv_results.std()))
print(name, np.round(cv_results, 3), 'Средняя точность: ', round(cv_results.mean(), 3))
# Графическое представление результатов
fig = plt.figure()
fig.suptitle('Точность, показанная классификаторами')
ax = fig.add_subplot(1, 1, 1)
plt.boxplot(results)
ax.set_xticklabels(names)
plt.show()
else:
x = x[:, 0:2] # Берем для отображения только две характеристики: длина и ширина чашелистика
n_classifiers = 4 # Число обучаемых классификаторов
plt.figure(figsize = (3 * 2, n_classifiers * 2))
plt.subplots_adjust(bottom = 0.2, top = 0.95)
xx = np.linspace(3, 9, 100)
yy = np.linspace(1, 5, 100).T
xx, yy = np.meshgrid(xx, yy)
Xfull = np.c_[xx.ravel(), yy.ravel()]
index = -1
for name, classifier in classifiers:
index += 1
if index < n_classifiers:
classifier.fit(x, y) # Обучение
y_pred = classifier.predict(x) # Оцениваем результат
accuracy = accuracy_score(y, y_pred)
print("Точность обучения %s: %0.1f%% " % (name, accuracy * 100))
# Показываем вероятности
probas = classifier.predict_proba(Xfull)
n_classes = np.unique(y_pred).size
for k in range(n_classes):
plt.subplot(n_classifiers, n_classes, index * n_classes + k + 1)
class_name = {
k == 0 : 'Setosa',
k == 1 : 'Versicolor',
k == 2 : 'Virginica'
}[True]
plt.title(class_name)
if k == 0:
plt.ylabel(name)
imshow_handle = plt.imshow(probas[:, k].reshape((100, 100)), extent = (3, 9, 1, 5), origin = 'lower')
plt.xticks(())
plt.yticks(())
idx = (y_pred == k)
if idx.any():
plt.scatter(X[idx, 0], X[idx, 1], marker = 'o', c = 'w', edgecolor = 'k')
ax = plt.axes([0.15, 0.04, 0.7, 0.05])
plt.title("Вероятность")
plt.colorbar(imshow_handle, cax = ax, orientation = 'horizontal')
plt.show()
Все классификаторы будут задействованы, если cross_val = True.
После выполнения классификации выводятся результаты (рис. 5):
SGD [1. 0.933 1. 0.8 0.267 0. 1. 0.933 1. 1. ] Средняя точность: 0.793
SVL [1. 1. 1. 0.867 0.867 0.733 1. 0.8 0.667 0.733] Средняя точность: 0.867
RF [1. 1. 1. 1. 0.867 0.867 1. 0.8 0.6 0.933] Средняя точность: 0.907
GP [1. 1. 1. 1. 0.867 0.867 1. 0.867 0.733 0.933] Средняя точность: 0.927
AB [1. 1. 1. 1. 0.933 0.867 1. 0.867 0.8 0.933] Средняя точность: 0.94
DT [1. 1. 1. 1. 0.933 0.867 1. 0.867 0.8 1. ] Средняя точность: 0.947
LR [1. 1. 1. 1. 0.933 0.867 1. 0.867 0.867 0.933] Средняя точность: 0.947
NB [1. 1. 1. 0.933 0.933 0.867 1. 0.867 0.867 1. ] Средняя точность: 0.947
SVR [1. 1. 1. 1. 0.867 0.867 1. 0.867 0.867 1. ] Средняя точность: 0.947
MLP [1. 1. 1. 1. 0.867 0.933 1. 0.867 0.667 1. ] Средняя точность: 0.933
KNN [1. 1. 1. 1. 0.867 0.867 1. 0.867 0.867 1. ] Средняя точность: 0.947
QDA [1. 1. 1. 1. 0.8 0.933 1. 1. 0.933 1. ] Средняя точность: 0.967
LDA [1. 1. 1. 1. 0.933 0.933 1. 1. 0.8 1. ] Средняя точность: 0.967
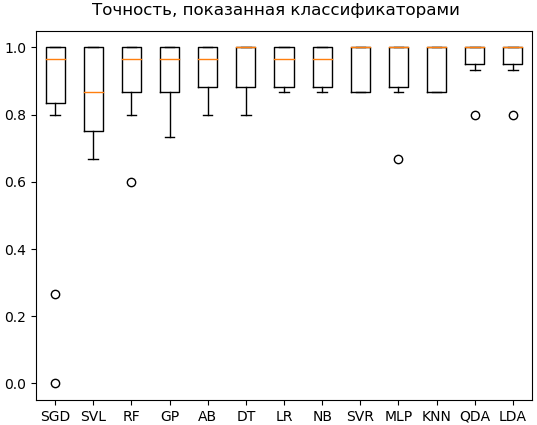
Рис. 5. Точность классификации
Если указать cross_val = False, тогда для 4-х классификаторов будут выведены карты вероятностей (рис. 6):
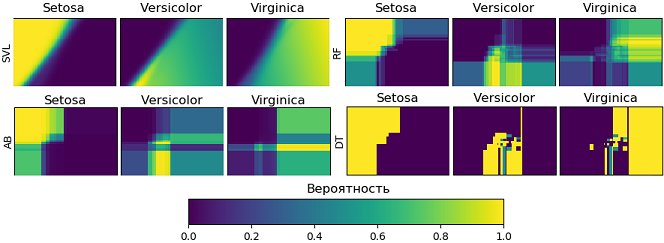
Рис. 6. Карты вероятностей для SVL, RF, AB и DT
Достигнутая точность классификации ниже, поскольку для обучения были использованы только две характеристики: длина и ширина чашелистика:
Точность классификации:
SVL: 79.3%
RF: 83.3%
AB: 72.0%
DT: 92.7%
Выполняется следующим кодом:
import numpy as np # for random
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # Для управления 3D-изображением (посредством мышки)
from sklearn import datasets
from sklearn import model_selection # for split
import keras # keras.utils.to_categorical
from keras.models import Sequential
from keras.layers import Dense
from keras import backend as K
#
def myLoss(y_true, y_pred):
return K.mean(K.square(y_pred - y_true))
#
seed = 348
np.random.seed(seed)
# Загружаем набор из библиотеки scikit-learn
iris = datasets.load_iris() # iris - dictionary-like object
X = iris.data
y = iris.target
# Выделяем обучающую и тестовую выборки
x_train, x_test, y_train, y_test = model_selection.train_test_split(X, y, test_size = 0.20) #, random_state = seed)
y_train = keras.utils.to_categorical(y_train, 3) # 3 - число классов; необязательный параметр
y_test_cat = keras.utils.to_categorical(y_test, 3)
# Создаем НС
model = Sequential()
model.add(Dense(units = 16, input_dim = 4, activation = 'relu'))
##model.add(Dense(48, activation = 'relu'))
##model.add(Dense(16, activation = 'relu'))
# softmax или sigmoid - функция активация нейрона последнего слоя
model.add(Dense(3, activation = 'softmax')) # softmax, sigmoid
##model.compile(loss = 'mse', optimizer = 'adam', metrics = ['accuracy']) # mean_squared_error, Adam
model.compile(loss = myLoss, optimizer = 'adam', metrics = ['accuracy']) # mean_squared_error, Adam
model.summary()
#
# Обучение нейронной сети
print('\nОбучение')
model.fit(x_train, y_train, epochs = 60, batch_size = 10, verbose = 0)
#
# Оценка результата
print('\nТестирование')
scores = model.evaluate(x_test, y_test_cat, verbose = 2)
#
print("%s: %.2f%%" % (model.metrics_names[0], scores[0]*100)) # loss (потери)
print("%s: %.2f%%" % (model.metrics_names[1], scores[1]*100)) # acc (точность)
#
# Прогноз
classes = model.predict_classes(x_test) # , batch_size = 10
# np.sum(classes == y_test) вернет сумму случаев, когда classes[i] = y_test[i]
# Поскольку в тестовой выборке 30 элементов (150 * 0.2), то для получения % пишем '/ 30.0 * 100'
accuration = np.sum(classes == y_test) / 30.0 * 100
print("Точность прогнозирования: " + str(accuration) + '%')
print("Прогноз:")
print(classes)
print("На самом деле:")
print(y_test)
if True:
# Выводим результаты наблюдений (по 3-м характеристикам)
fig = plt.figure(1, figsize = (5, 4))
ax = Axes3D(fig, rect = [0, 0, .95, 1], elev = 48, azim = 134)
for name, label in [('Setosa', 0), ('Versicolor', 1), ('Virginica', 2)]:
ax.text3D(X[y == label, 3].mean(),
X[y == label, 0].mean(),
X[y == label, 2].mean() + 2, name,
horizontalalignment = 'center',
bbox = dict(alpha = 0.2, edgecolor = 'w', facecolor = 'w'))
ax.scatter(X[:, 3], X[:, 0], X[:, 2], c = y, edgecolor = 'k')
ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([])
ax.set_xlabel('Ширина лепестка')
ax.set_ylabel('Длина чашелистика')
ax.set_zlabel('Длина лепестка')
ax.set_title('Ирисы Фишера')
ax.dist = 12
fig.show()
Получены следующие результаты:
Тестирование:
loss: 3.55%
acc: 100.00%
Точность прогнозирования: 100.0%
Прогноз:
[0 1 0 1 2 0 1 2 2 0 0 2 0 2 1 0 0 1 1 1 1 2 0 1 2 0 0 2 2 1]
На самом деле:
[0 1 0 1 2 0 1 2 2 0 0 2 0 2 1 0 0 1 1 1 1 2 0 1 2 0 0 2 2 1]