Список работ

Реализация алгоритмов Дейкстры и Левита

Курсовая работа

Иванова А. М., A-13-03, alibi_@mail.ru

Содержание

• Введение
• Представление данных
• Алгоритм Дейкстры
  • Описание алгоритма
  • Реализация алгоритма на языке программирования FPTL
• Алгоритм Левита
  • Описание алгоритма
  • Реализация алгоритма на языке программирования FPTL
• Тестирование программ
• Сравнение FPTL-реализаций алгоритмов Дейкстры и Левита
• Заключение
• Приложение 1. FPTL-код вспомогательных функций
• Приложение 2. Справка по языку программирования FPTL
• Приложение 3. Интерпретатор и компилятор FPTL
• Источники

Введение

В работе приводятся реализации алгоритмов Дейкстры и Левита нахождения кратчайших путей от заданной вершины до всех остальных вершин графа.
Алгоритмы реализованы на языке программирования FPTL
Интерпретатор FPTL пользуется особенностями языка для поиска параллельно вычисляемых функциональных переменных и обеспечивает их параллельную обработку на доступных вычислительных ресурсах.

Представление данных

• представление графа;
• N - количество вершин графа;
• S - номер начальной вершины.

• список весов минимальных путей от заданной вершины до всех остальных вершин;
• P - список предков: P[V] содержит номер вершины, имеющей общее ребро с вершиной V и принадлежащей кратчайшему пути от вершины S до вершины V.

Список P предков вершин позволяет восстановить кратчайший путь от заданной вершины S до любой иной вершины графа. Список вершин SX, образующих кратчайший путь от вершины S до вершины X, можно вычислить следующим образом:

Start:
 i = 0;
 SX[0] = X;
 V = P[X];
Begin:
 If (V == S) jump End;
 SX[i++] = V;
 jump Begin;
End.

Граф, содержащий N вершин, можно представить как список из N элементов вида:

<номер смежной вершины> * <веса ребра>

FPTL-тип элемента следующий:

Data para
{
 d = int * real;
}

Сам же список, представляющий граф, описывается в FPTL в виде следующего параметризованного типа данных:

Data list['x]
{
 Constructors
 {
  =>list : c_nil;
  'x*list['x] => list['x] : c_cons;
 }
 list = c_nil ++ ('x * list).c_cons;
}

Возьмем в качестве примера следующий граф (рис. 1).

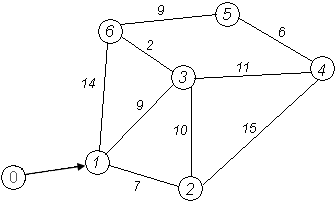
Рис. 1. Вариант тестового графа

Приведем отвечающий этому графу FPTL-список:

list[list[para]]: Gr1 =
/*0*/( ((1 * 14.0) * c_nil ).c_cons *
/*1*/( ((2 * 7.0) * ((3 * 9.0) * ((6 * 14.0) * c_nil ).c_cons).c_cons).c_cons *
/*2*/( ((1 * 7.0) * ((3 * 10.0) * ((4 * 15.0) * c_nil ).c_cons).c_cons).c_cons *
/*3*/( ((1 * 9.0) * ((2 * 10.0) * ((4 * 11.0) * ((6 * 2.0) * c_nil ).c_cons).c_cons).c_cons).c_cons *
/*4*/( ((2 * 15.0) * ((3 * 11.0) * ((5 * 6.0) * c_nil ).c_cons).c_cons).c_cons *
/*5*/( ((4 * 6.0) * ((6 * 9.0) * c_nil ).c_cons).c_cons *
/*6*/( ((1 * 14.0) * ((3 * 2.0) * ((5 * 9.0) * c_nil ).c_cons).c_cons).c_cons * c_nil ).c_cons).c_cons).c_cons).c_cons).c_cons).c_cons).c_cons;

Алгоритм Дейкстры

Описание алгоритма

Пусть дан граф, число вершин в котором равно N, и дана вершина S, из которой ищутся пути. Определим массив D[1..N], который после завершения алгоритма будет содержать длины кратчайших путей от вершины S (D[X] – это текущая длина кратчайшего пути от вершины S до вершины X). Сначала массив D заполним значениями "бесконечность", за исключением элемента, отвечающего вершине S, положив D[S] = 0. Алгоритм Дейкстры состоит из N итераций, каждая из которых будет пытаться улучшить значения D.
В начале алгоритма все вершины помечаются как непосещённые. Если все вершины посещены, то алгоритм завершается. Иначе – из непосещённых вершин выбирается такая вершина X, которая имеет минимальное значение D[X]. Далее рассмотрим всевозможные ребра, выходящие из X и входящие в непомеченные вершины, и попытаемся улучшить значения D вдоль каждого ребра. Затем пометим вершину X как посещенную и выполним следующую итерацию.
Алгоритм Дейкстры не может быть употреблен, если в графе имеются ребра с отрицательными весами. Будем, к примеру, в графе, приведенном на рис. 2, искать кратчайшие пути от вершины 1 до всех прочих вершин.

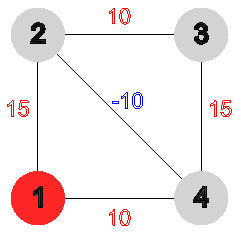
Рис. 2. В графе с отрицательными весами ребер для поиска кратчайших путей следует употребить алгоритм Левита

Алгоритм Дейкстры укажет, что до вершины 4 кратчайшим является путь, проходящий через ребро, соединяющее вершины 1 и 4. На самом деле путь, проходящий через вершины 1, 2 и 4, в два раза короче.

Реализация алгоритма на языке программирования FPTL

В приводимом ниже листинге опущены вспомогательные функции (см. прил. 1).

Scheme find_paths
{
 @ = REZ;
 LIMIT = <65535>;
 // Помеченные вершины
 ZERO = (NV * <c_nil> * <0>).create_list;
 M = (ZERO * VBEG * <1>).put_elem;
 // Создаем список с весами путей
 WTEMP = (NV * <c_nil> * LIMIT).create_list;
 W = (WTEMP * VBEG * <0>).put_elem;
 // Сохранение путей
 G = (NV * <c_nil> * VBEG).create_list;
 // Обьявляем текущей начальную вершинe и входим в основной алгоритм
 REZ = (M * W * G * GRAF * VBEG).step_Dijkstra;
 // Генерация сильно связного графа (для тестов)
 //GRAF1 = (NV * <c_nil> * NV).Strongly_communication_graf;
 VBEG = I(3,3);
 NV = I(2,3);
 GRAF = I(1,3);
Fun step_Dijkstra
{
 step_Dijkstra = PEXIT -> WG_NEW
+ PEXIT.not -> (M_NEW * WG_NEW * GRAF * TEMP_NEW).step_Dijkstra;
 PEXIT = (<-1> * TEMP_NEW).eq;
 // Берем вершины, смежные с текущей вершиной TEMP
 SM_VERTEX = (GRAF * TEMP).get_elem;
 // (W * G): пересчитываем веса и пути
 WG_NEW = (SM_VERTEX * M * W * G * TEMP * WES_TEMP).re_calculat_wg;
 // Помечаем вершину как рассмотренную
 M_NEW = (M * TEMP * <1>).put_elem;
 // Смотрим вес текущей вершины
 WES_TEMP = (W * TEMP).get_elem;
 // Получаем наименьшую по весу непосещенную вершину
 LIMIT = <65535>;
 TEMP_NEW = (M_NEW * WG_NEW.I(1,2) * LIMIT * <-1> * <0>).min_no_mask;
 M = I(1,5);
 W = I(2,5);
 G = I(3,5);
 GRAF = I(4,5);
 TEMP = I(5,5);
 Fun min_no_mask
 {
  min_no_mask = PEXIT -> NOM_MIN + (M.cdr * W.cdr * MIN_NEW * NOM_MIN_NEW * NOM).min_no_mask;
  PEXIT = M.~c_nil;
  MIN_NEW = P.not -> MIN + P -> W.car;
  NOM_MIN_NEW = P.not -> NOM_MIN + P -> NOM_TEMP;
  P = (PM * P2).and;
  PM = (M.car * <0>).eq;
  P2 = (W.car * MIN).lt;
  NOM = (NOM_TEMP * <1>).plus;
  M = I(1,5);
  W = I(2,5);
  MIN = I(3,5);
  NOM_MIN = I(4,5);
  NOM_TEMP = I(5,5);
 }
 Fun re_calculat_wg
 {
  re_calculat_wg = PEXIT -> (W * G) + REZ;
  // Не покидаем функцию, пока не проверим все смежные вершины
  PEXIT = I(1,6).~c_nil;
  REZ = P -> (SM_VERTEX.I(3,3) * M * W_NEW * G_NEW * TEMP * WES_TEMP).re_calculat_wg
   + P.not -> (SM_VERTEX.I(3,3) * M * W * G * TEMP * WES_TEMP).re_calculat_wg;
  P = (PM * PW).and;
  // Проверяем, не помечена ли вершина
  PM = ((M * VERTEX).get_elem * <0>).eq;
  // Проверяем, нашли ли мы лучший вес
  PW = (WES_OLD * WES).gt;
  WES_OLD = (W * VERTEX).get_elem;
  WES_R = SM_VERTEX.I(2,3);
  WES = (WES_TEMP * WES_R).plus;
  VERTEX = SM_VERTEX.I(1,3);
  W_NEW = (W * VERTEX * WES).put_elem;
  G_NEW = (G * VERTEX * TEMP).put_elem;
  SM_VERTEX = I(1,6).~c_cons;
  M = I(2,6);
  W = I(3,6);
  G = I(4,6);
  TEMP = I(5,6);
  WES_TEMP = I(6,6);
 }
}
}

Алгоритм Левита

Описание алгоритма

Пусть массив D[1..N] будет содержать текущие кратчайшие длины путей от вершины S до прочих вершин графа, то есть D[X] – это текущая длина кратчайшего пути от вершины S до вершины X. Изначально массив D заполнен значениями "бесконечность", кроме D[S] = 0. После завершения работы алгоритма этот массив будет содержать искомые кратчайшие расстояния.
Пусть массив P[1..N] содержит текущих предков, то есть P[X] – это вершина, предшествующая вершине X в кратчайшем пути от вершины S до вершины X. Так же как и массив D, массив P изменяется постепенно по ходу алгоритма и к концу его принимает окончательные значения.
На каждом шаге алгоритма Левита поддерживается три множества вершин:

• M₀ – вершины, расстояние до которых уже вычислено (но, возможно, не окончательно);
• M₁ – вершины, расстояние до которых вычисляется;
• M₂ – вершины, расстояние до которых ещё не вычислено.

Вершины множества M₁ хранятся в виде двунаправленной очереди.
Изначально все вершины помещаются во множество M₂, кроме вершины S, которая помещается во множество M₁.
На каждом шаге алгоритма берется верхний элемент очереди M₁. Пусть V – это выбранная вершина. Переводим V во множество M₀. Затем просматриваем все рёбра, выходящие из V. Пусть вершина T – это второй конец текущего, выходящего из V ребра, а L – это его вес.
Если T принадлежит M₂, то вершину T переносим во множество M₁, помещая ее в конец очереди. D[T] полагаем равным D[V] + L.
Если T принадлежит M₁, то пытаемся улучшить значение D[T]: D[T] = min(D[T], D[V] + L). Сама вершина T в очереди не передвигается.
Если T принадлежит M₀ и если D[T] можно улучшить (D[T] > D[V] + L), то улучшаем D[T], а вершину T возвращаем во множество M₁, помещая ее в начало очереди.
Разумеется, при каждом обновлении массива D следует обновлять и массив P.
Алгоритм Левита, в отличие от алгоритма Дейкстры, работает с ребрами, имеющими отрицательный вес: при обнаружении более короткого пути проблемная вершина будет перенесена из M0 в M1.

Реализация алгоритма на языке программирования FPTL

В листинге не приведены вспомогательные функции (см. прил. 1).

Scheme find_paths
{
 @ = REZ;
 LIMIT = <65535>;
 M0 = <c_nil>;
 M1 = (<c_nil> * VBEG).push_begin;
 M2 = (INCR * VBEG).del_elem;
 INCR = (NV * <c_nil>).create_list_incr;
 // Создаем список с весами путей
 WTEMP = (NV * <c_nil> * LIMIT).create_list;
 W = (WTEMP * VBEG * <0>).put_elem;
 // Сохранение путей
 G = (NV * <c_nil> * VBEG).create_list;
 // Входим в основной алгоритм
 REZ = (M0 * M1 * M2 * W * G * GRAF).step_Levita;
 // Генерация сильно связного графа (для тестов)
 // GRAF1 = (NV * <c_nil> * NV).Strongly_communication_graf;
 VBEG = I(3,3);
 NV = I(2,3);
 GRAF = I(1,3);
Fun step_Levita
{
 step_Levita = PEXIT -> (W * G) + PEXIT.not -> (MMMWG * GRAF).step_Levita;
 PEXIT = M1.~c_nil -><true> + M1.~c_cons -> <false>;
 // Берем первую вершину в M1
 V = M1.car;
 // Переносим ее в M0
 M0_NEW = (V * M0).c_cons;
 M1_NEW = M1.cdr;
 // Берем смежные вершины
 SM_VERTEX = (GRAF * V).get_elem;
 // Смотрим вес текущей вершины
 WES_V = (W * V).get_elem;
 // Улучшаем веса остальных вершин
 MMMWG = (SM_VERTEX * M0_NEW * M1_NEW * M2 * W * G * V * WES_V).re_calculat_wg;
 M0 = I(1,6);
 M1 = I(2,6);
 M2 = I(3,6);
 W = I(4,6);
 G = I(5,6);
 GRAF = I(6,6);
 Fun re_calculat_wg
 {
  re_calculat_wg = PEXIT -> (M0 * M1 * M2 * W * G) + PEXIT.not -> (SM_VERTEX.I(3,3) *
   MMM * W_NEW * G_NEW * V * WES_V).re_calculat_wg;
  // Не покидаем функцию, пока не проверим все смежные вершины
  PEXIT = I(1,8).~c_nil -><true> + I(1,8).~c_cons -> <false>;
  T = SM_VERTEX.I(1,3); //номер смежной вершины
  L = SM_VERTEX.I(2,3); //вес ребра
  WT_NEW = (WES_V * L).plus; //возможное новое значение
  WT_OLD = (W * T).get_elem; //текущее значение
  P_MIN = (WT_NEW * WT_OLD).lt; // Условие улучшения значения
  P_TINM0 =(M0 * T * <0>).find_elem; // Условие принадлежности M0
  P_TINM1 =(M1 * T * <0>).find_elem; // Условие принадлежности M1
  P_TINM2 =(M2 * T * <0>).find_elem; // Условие принадлежности M2
  // Если T принадлежит M2, то T переносим во множество M1 в конец очереди
  // WT полагаем равным WV + L.
  PTM2 = P_TINM2.I(1,2);
  M1_NEW1 = PTM2 -> (M1 * T).push_back + PTM2.not -> M1;
  M2_NEW1 = PTM2 -> (M2 * P_TINM2.I(2,2)).del_elem + PTM2.not -> M2;
  // Если T принадлежит M1, то пытаемся улучшить значение WT
  // WT = min (WT, WV + L). Сама вершина T никак не передвигается в очереди
  // Если T принадлежит M0, и если WT можно улучшить (WT > WV + L),
  // то улучшаем WT, а вершину T возвращаем в множество M1,
  // помещая ее в начало очереди
  PTM0 = P_TINM0.I(1,2);
  M0_NEW2 = PTM0 -> (M0 * P_TINM0.I(2,2)).del_elem + PTM0.not -> M0;
  M1_NEW2 = PTM0 ->(T * M1).c_cons -> PTM0.not ->M1;
  // Условие изменения весов
  PGW = (PTM2 * P_MIN).or;
  W_NEW = PGW -> (W * T * WT_NEW).put_elem + PGW.not -> W;
  G_NEW = PGW -> (G * T * V).put_elem + PGW.not -> G;
  // Условие перенова в другие группы (M0_NEW * M1_NEW * M2_NEW)
  PM2 = (P_TINM0.I(1,2) * P_MIN).and;
  MMM = PM2 -> (M0_NEW2 * M1_NEW2 * M2) + PM2.not -> MMM_ELSE;
  PM1 = PTM2;
  MMM_ELSE = PM1 -> (M0 * M1_NEW1 * M2_NEW1) + PM1.not -> (M0 * M1 * M2);
  SM_VERTEX = I(1,8).~c_cons;
  M0 = I(2,8);
  M1 = I(3,8);
  M2 = I(4,8);
  W = I(5,8);
  G = I(6,8);
  V = I(7,8);
  WES_V = I(8,8);
  }
 }
}

Тестирование программ

Найдем в приведенном на рис. 1 графе кратчайшие пути от вершины 1 до всех остальных вершин.
Запускаемая программа имеет следующий вид:

Functional Program find_paths
<здесь размещается FPTL-реализация алгоритма Дейкстры или Левита>
Application
list[list[para]]: Gr1 =
/*0*/( ((1 * 14.0) * c_nil ).c_cons *
/*1*/( ((2 * 7.0) * ((3 * 9.0) * ((6 * 14.0) * c_nil ).c_cons).c_cons).c_cons *
/*2*/( ((1 * 7.0) * ((3 * 10.0) * ((4 * 15.0) * c_nil ).c_cons).c_cons).c_cons *
/*3*/( ((1 * 9.0) * ((2 * 10.0) * ((4 * 11.0) * ((6 * 2.0) * c_nil ).c_cons).c_cons).c_cons).c_cons *
/*4*/( ((2 * 15.0) * ((3 * 11.0) * ((5 * 6.0) * c_nil ).c_cons).c_cons).c_cons *
/*5*/( ((4 * 6.0) * ((6 * 9.0) * c_nil ).c_cons).c_cons *
/*6*/( ((1 * 14.0) * ((3 * 2.0) * ((5 * 9.0) * c_nil ).c_cons).c_cons).c_cons * c_nil ).c_cons).c_cons).c_cons).c_cons).c_cons).c_cons).c_cons;
%find_paths(Gr1, 7, 1)

Результаты выполнения программ реализаций алгоритмов Дейкстра и Левита совпадают:

(65535*(0*(7.0*(9.0*(20.0*(20.0*(11.0*c_nil).c_cons).c_cons).c_cons).c_cons).c_cons).c_cons).c_cons*(1*(1*(1*(1*(3*(6*(3*c_nil).c_cons).c_cons).c_cons).c_cons).c_cons).c_cons).c_cons

или в табличном представлении:

Вес пути = 65535 (0xffff) обозначает, что фиктивная вершина 0 исключена из пространства поиска решений.

Сравнение FPTL-реализаций алгоритмов Дейкстры и Левита

FPTL-реализации алгоритмов Дейкстры и Левита сравнивались по двум следующим параметрам:

• время вычислений;
• потребляемая память.

Программы запускались на семействе сильно связных графов, для генерации которых использовалась приведенная в прил. 1. функция Strongly_communication_graf.
Полученные результаты иллюстрируют рис. 3 и рис. 4.

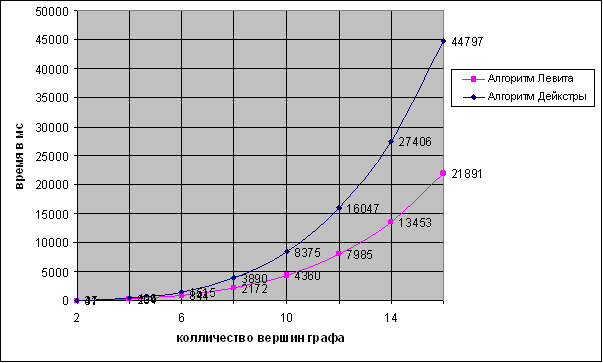
Рис. 3. Зависимость времени вычислений от количества вершин в графе

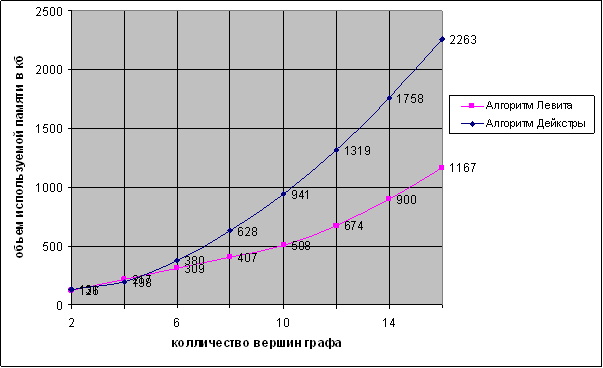
Рис. 4. Зависимость используемой памяти от количества вершин в графе

Заключение

Рассмотрены алгоритмы Дейкстры и Левита нахождения кратчайших путей в графе от заданной вершины до всех остальных вершин.
Из рис. 3 и 4 видно, что алгоритм Левита и по быстродействию, и по потребляемой памяти превосходит алгоритм Дейкстры. Таким образом, при решении задачи поиска кратчайших путей в графе от заданной вершины до всех его прочих вершин следует отдать предпочтение алгоритму Левита.

Приложение 1. FPTL-код вспомогательных функций

// Генерация сильно связного графа
Fun Strongly_communication_graf
{
 Strongly_communication_graf = P -> GRAF + P.not -> (DEC * G * KOL).Strongly_communication_graf;
 P = (NOM * <0>).eq;
 G = ((KOL * <c_nil> * <1> * DEC).create_list_para * GRAF).c_cons;
 DEC = (NOM * <1>).minus;
 NOM = I(1,3);
 GRAF = I(2,3);
 KOL = I(3,3);
 Fun create_list_para
 {
  create_list_para = P -> LIST + P.not -> REZ;
  P = (NOM * <0>).eq;
  DEC = (NOM * <1>).minus;
  PV = (VERTEX * DEC).ne;
  REZ = PV -> (DEC * ((DEC * MASKA) * LIST).c_cons * MASKA * VERTEX).create_list_para + PV.not -> (DEC * LIST * MASKA * VERTEX).create_list_para;
  NOM = I(1,4);
  LIST = I(2,4);
  MASKA = I(3,4);
  VERTEX = I(4,4);
 }
}
// Пополняет список заданным количеством элементов
// (<количество элементов>, <первоначальный список>, <инкремент>)
Fun create_list_incr
{create_list_incr = PEXIT.not -> LREZ + PEXIT -> LIST_TEMP;
 PEXIT = (NOM * <1>).lt;
 LREZ = (DEC * LIST).create_list_incr;
 LIST = (DEC * LIST_TEMP).c_cons;
 DEC = (NOM * <1>).minus;
 NOM = I(1,2);
 LIST_TEMP = I(2,2);
}
// Инициализирует список заданным количеством элементов
// (<количество элементов>, <первоначальный список>)
Fun create_list
{create_list = PEXIT.not -> LREZ + PEXIT -> LIST_TEMP;
 PEXIT = (NOM * <1>).lt;
 LREZ = LAST.create_list;
 LAST = (DEC * LIST * MASK);
 LIST = (MASK * LIST_TEMP).c_cons;
 DEC = (NOM * <1>).minus;
 NOM = I(1,3);
 LIST_TEMP = I(2,3);
 MASK = I(3,3);
}
// Первый элемент списка
Fun car
{
 car = ~c_cons.I(1,2);
}
// Получение хвоста списка
Fun cdr
{
 cdr = ~c_cons.I(2,2);
}
// Вычисление длинны списка
Fun leng
{
 leng = ~c_nil -> <0> + (cdr.leng * <1>).plus;
}
// Получение i-го элемента (<список>, <номер элемента>)
// Нумерация элементов ведется с нуля
Fun get_elem
{
 get_elem = PEXIT.not -> EREZ + PEXIT -> ELEMENT;
 PEXIT = (NOM * <1>).lt;
 EREZ = (LISTNEXT * DEC).get_elem;
 DEC = (NOM * <1>).minus;
 LISTNEXT = LIST.cdr;
 ELEMENT = LIST.car;
 LIST = I(1,2);
 NOM = I(2,2);
}
// Замена i-го элемента (<список> * <номер элемента> * <новое значение>)
// Нумерация элементов ведется с нуля
Fun put_elem
{
 put_elem = PEXIT.not -> (ELEMENT * LIST).c_cons + PEXIT -> (ZAMENA * I(1,3).cdr).c_cons;
 PEXIT = (NOM * <1>).lt;
 DEC = (NOM * <1>).minus;
 ELEMENT = I(1,3).car;
 LIST = (I(1,3).cdr * DEC * ZAMENA).put_elem;
 NOM = I(2,3);
 ZAMENA = I(3,3);
}
// Добавляет элемент в начало списка
Fun push_begin
{
 push_begin = (I(2,2) * I(1,2)).c_cons;
}
// Добавляет элемент в конец списка
Fun push_back
{
 push_back = P -> (I(2,2) * <c_nil>).c_cons + P.not -> (I(1,2).car * (I(1,2).cdr * I(2,2)).push_back).c_cons;
 P = I(1,2).~c_nil -> <true> + I(1,2).~c_cons -> <false>;
}
// Удаляет последний элемент списка
Fun del_back
{
 del_back = P -> <c_nil> + P.not -> (car * cdr.del_back).c_cons;
 P = cdr.~c_nil -> <true> + cdr.~c_cons -> <false>;
}
// Удаляет i-й элемент без проверки существования этого элемента
Fun del_elem
{
 del_elem = P -> L.cdr + P.not -> (L.car * (L.cdr * DEC).del_elem).c_cons;
 P = (NOM * <0>).eq;
 DEC = (NOM * <1>).minus;
 L = I(1,2);
 NOM = I(2,2);
}
// Возвращает true и номер элемента Е, если элемент имеется в списке
Fun find_elem
{
 find_elem = L.~c_nil -> (<false> * <0>) + REZ_NEW;
 REZ_NEW = P.not -> (L.cdr * E * INC).find_elem + P -> (<true> * REZ);
 P = (E * L.car).eq;
 INC = (<1> * REZ).plus;
 L = I(1,3);
 E = I(2,3);
 REZ = I(3,3);
}

Приложение 2. Справка по языку программирования FPTL

Язык программирования FPTL (Functional Programming Typified Language) разработан профессорами МЭИ Кутеповым В.  П. и Фальком В.  Н. Основное назначение языка – это выполнение высокопроизводительных вычислений.
FPTL-программа базируется на функциях. Тип функции записывается следующим образом:

T_in => T_out,

где T_in – тип входных данных, а T_out – тип выходных данных.

Встроенные функции FPTL

Операции композиции функций

FPTL содержит три операции композиции функций:

• Точка: F1.F2 – последовательное применение сначала функции F1 к исходным данным, а потом функции F2 к результату функции F1.
• Звездочка: F1*F2 – независимое вычисление функций F1 и F2, принимающим аргумент операции (в общем случае имеем: F1*…*Fn). Эта операция является источником параллелизма – каждую функцию Fi можно вычислять параллельно.
• Условная операция: P -> F1, F2. Если P есть истина, то результатом операции является F1, иначе – F2. Операция также является источником параллелизма – можно выполнить вычисление значений функций F1 и F2 вместе с вычислением условия P. После вычисления значения условия ненужнй поток (F1 или F2) прерывается.

Типы данных

Встроенные типы данных: bool, int, real и string.
Также можно объявлять синоним, создавать кортеж и употреблять конструктор типа данных.

Пример создания синонима встроенного типа данных:

Data d
{
 d = int;
}

Пример создания кортежа:

Data d
{
  d = string * int * int;
}

Кортежи могут содержать несколько компонент, например:

Data Person
{
 Person = name * age;
 name = string;
 age = int;
}

При создании производных типов данных применяются конструкторы следующего вида:

Имя компоненты => имя производного типа данных : имя конструктора;

Имена всех конструкторов предваряются префиксом c_.
Пример создания производного типа данных с конструкторами:

Data Nat
{
Constructors
 {
  => Nat : c_null;
  Nat => Nat : c_succ;
 }
 Nat = c_null ++ (Nat).c_succ;
}

Тип Nat имеет два конструктора: c_null и c_succ.
В соответствии с последнней строкой описания типа данных Nat значение типа Nat может определяться либо конструктором c_null, либо конструктором c_succ, употребленным с данным типа Nat, например:

c_null
((c_null).c_succ).c_succ.

Можно также создавать типы данных с параметрами (параметризованные типы). Имя параметра предваряется апострофом и указывается в квадратных скобках после имени типа данных. Например тип данных список объявляется следующим образом:

Data list['x]
{
 Constructors
 {
  =>list : c_nil;
  'x*list['x] => list['x] : c_cons;
 }
 list = c_nil ++ ('x * list).c_cons;
}

Параметры типа данных могут иметь параметризованный тип.

Описание программы

Код программы вычисления факториала выглядит следующим образом:

Functional Program factorial
Scheme factorial
{
 factorial = P -> F1, F2;
 P = (id*<0>).eq;
 F1 = <1>;
 F2 = (id * DEC.@) . mult;
 DEC = (id*<1>).minus;
}
Application
%factorial(8)

Выпоняемые программой действия записываются в блоке Scheme, содержащем последовательность функциональных уравнений.
Функциональные уравнения записываются с новой строки. Точкой входа в программу является функциональная переменная (ФП) с именем, совпадающим с именем схемы. Имена прочих ФП состоят из прописных букв и цифр.
Каждое функциональное уравнение имеет вид:

Имя ФП = описание ФП;

В описании ФП можно использовать операции композиции, функциональные переменные, определенные в схеме, а также встроенные функции FPTL.
В аргументы ФП передаются неявно. Например, аргументы функциональной переменной factorial будут переданы в функциональные переменные P, F1, F2 при их вычислении.
Получить значение аргумента можно, употребив либо функцию id, либо функцию I(m, n), возвращающую аргумент с номером m из n входных аргументов.
В программе может быть использован символ @. Он является синонимом ФП с именем, совпадающим с именем схемы.
Вызов программы производится в секции Application:

Application
%factorial(8)

Секция Application может содержать описание переменных, принимаемых программой. Описание переменной в секции Application имеет вид:

Тип переменной : имя переменной = значение переменной;

Приложение 3. Интерпретатор и компилятор FPTL

Кластерный интерпретатор позволяет выполнять программы FPTL на любом кластере машин, на которых установлены Java Runtime Environment и пакеты среды выполнения языка FPTL. Связь между машинами осуществляется посредством сокетов.
Интерпретатор пользуется особенностями языка FPTL для поиска параллельно вычисляемых функциональных переменных (ФП).

Интерпретатор имеет следующие отличительные черты:

• Поддержка сетей любого размера.
• Поддержка любой пропускной способности сети.
• Поддержка любого числа процессоров/ядер на машине.
• Автоматический поиск ФП.
• Функционал по поиску и использованию в процессе вычислений запоминаемых ФП, – таких, что если F(a) уже вычислено, то при следующей попытке вычисления F(a) будет использован сохраненный результат.
• Работа на куче, а не на стеке, что упрощает выполнение рекурсивных алгоритмов.
• Использование для оптимизации переноса вычисляемых ФП информации о загруженности как отдельной машины, так и кластера.
• Возможность динамического добавления новых машин в кластер в процессе вычисления (они сразу же смогут быть использованы системой).
• Динамическое управление выполнением функций в зависимости от загруженности машин кластера (раздельное внутримашинное и кластерное управление).

Компилятор FPTL переводит программы с языка FPTL на исходный код языка Java. Затем для окончательной обработки программы FPTL-компилятор вызывает Java-компилятор.

Источники

1. Дейкстра Э. Дисциплина программирования. – М.: Мир, 1978. – 275 с.
2. Романовский И. В. Дискретный анализ: Учебное пособие для студентов, специализирующихся на прикладной математике и информатике. – СПб.: Невский Диалект; БХВ-Петербург, 2003. – 320 с.
3. wikipedia.org

Список работ