Показать возможность применения генетического алгоритма для решения задачи оптимизации расписания движения трамваев. В качестве критерия оптимизации используется сумма среднего времени ожидания (в секундах) и числа рейсов расписания.
Задача решается при следующих допущениях:
Расписание задается в виде следующего массива:
S = {t1, t2, …, tm},
где
ti – время отправления рейса i с начальной (конечной) остановки маршрута;
m – суточное число рейсов на маршруте.
В этом массиве неизменными являются значения t1 и tm – соответственно время первого и последнего рейсов. Прочие элементы могут в процессе решения задачи изменяться.
Значение m определяет размерность решаемой задачи. В случае одного маршрута, если t1 = 5 час и tm = 24 час и среднее время между рейсами составляет 3 мин, то m = 380.
Популяция – это множество расписаний:
P = {S1, S2, …, Sn},
Расписания генерируются по следующему правилу:
tj + 1 = tj + Δt,
где Δt = rand(tmin, tmax),
где tmin, tmax – соответственно минимально и максимально допустимые промежутки между рейсами (задаются разными для часов пик, утренних, вечерних и дневных часов движения).
Минимизируется сумма среднего времени ожидания (в секундах) и числа рейсов расписания.
Время ожидания рассчитывается следующим образом:
T = ΣRk = 1Σni = 1Wi / Σni = 1Ni
где R – число рейсов в расписании;
n – число остановок на маршруте;
Wi – время ожидания трамвая на остановке i;
Ni – число пассажиров, севших в трамвай на остановке i.
В свою очередь, расчет Wi ведется по следующей формуле:
Wi = Tij – Tij – 1,
где Tij – время отправления рейса j с остановки i.
Время прибытия рейса j на останову i равно:
T ji0 = Tij – 1 + i - 1, i * di - 1, i,
где vi - 1, i – средняя скорость движения трамвая между остановками i - 1 и i;
di - 1, i – расстояние между остановками i - 1 и i.
Tij = T ji0 + TOij,
где TOij – время посадки пассажиров, ожидающих на остановке, в прибывший трамвай.
TOij = to * Nij
где to – среднее время посадки одного пассажира;
Nij – число пассажиров, севших в трамвай рейса j на остановке i.
Полагается, что в трамвай входят все находящиеся на остановке пассажиры.
Число пассажиров, ожидающих трамвай, и число пассажиров, его покидающих, – это случайная величина, для работы с которой используются диаграммы прихода/выхода пассажиров.
Диаграммы формируются для каждой остановки на основе статистических данных отдельно для рабочих дней, выходных и праздников.
Пример диаграммы показан на рис. 1.
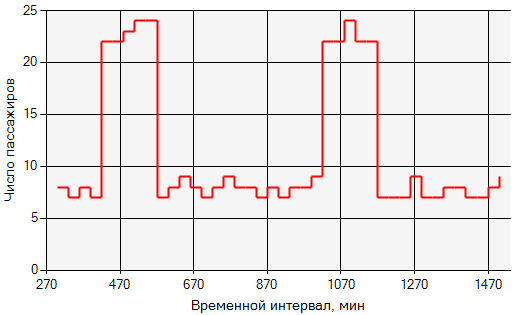
Рис. 1. Диаграмма прихода пассажиров (рабочий день)
Каждый временной интервал диаграммы показывает, сколько пассажиров пришло на остановку в этот интервал.
Диаграмма позволяет найти число пассажиров, пришедших на остановку в промежуток между двумя соседними рейсами. Если этот промежуток принадлежит интервалу диаграммы, то это число равно:
NCij = NTij * (Tij– T ij – 1) / ΔT
гдеΔT – длина временного интервала диаграммы;
NTij – показание диаграммы (число пассажиров, приходящих на остановку в рассматриваемый интервал).
Если же промежуток между двумя соседними рейсами принадлежит нескольким интервалам диаграммы, то при вычислении числа пришедших пассажиров учитывается вклад каждого интервала.
Аналогично оценивается и число пассажиров, выходящих из трамвая.
В работе диаграммы прихода/выхода генерируются автоматически. Программа их построения описана в [1].
Применительно к решаемой задаче генетический алгоритм записывается следующим образом:
Реализованное на C# приложение позволяет искать расписания как при движении с турникетами, так и без них.
Выбор варианта расчета указывается в форме, приведенной на рис. 2.
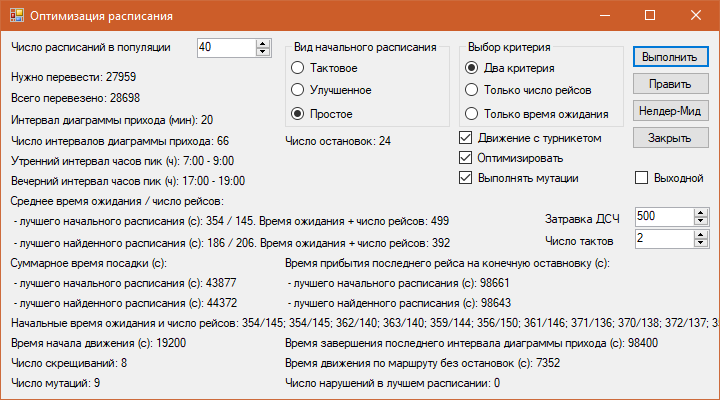
Рис. 2. Пользовательский интерфейс
При движении с турникетами имеем следующие значения критериев:В случае тактовых расписаний [4] генетический алгоритм неприменим, поскольку и мутации, и перестройки расписания сделают начальное тактовое расписание не тактовым. Поэтому в приложение встроен код, обеспечивающий оптимизацию тактового расписания с помощью метода Неллдера-Мида [5].
График прибытия трамваев на остановку i рассчитывается так же, как и для нетактового расписания.
Время прибытия рейса j на останову i равно:
T ji0 = Tij – 1 + vi - 1, i * di - 1, i,
где T ji - 1 – время отправления рейса j с остановки i - 1,
vi - 1, i – средняя скорость движения трамвая между остановками i - 1 и i;
di - 1, i – расстояние между остановками i - 1 и i.
Tij = T ji0 + TOij,
где TOij – время посадки пассажиров, ожидающих на остановке, в прибывший трамвай.
TOij = to * Nij
где to – среднее время посадки одного пассажира;
Nij – число пассажиров, севших в трамвай рейса j на остановке i.
Алгоритм Нелдера-Мида реализует безусловную оптимизацию. При составлении расписания должны быть соблюдены ограничения на максимально и минимально допустимые интервалы между соседними рейсами.
В случае тактового расписания интервал между рейсами определяется размером такта. Соблюдение ограничений на размер такта обеспечивается следующими модификациями алгоритма:
// Tмин, Tмакс – минимально и максимально допустимые размеры тактов
// Тi – текущее значение i-го такта
Если Тi < Tмин Тогда
Тi = Tмин
КонецЕсли
Если Тi > Tмакс Тогда
Тi = Tмакс
КонецЕсли
Иными словами, размер такта, нарушившего ограничение, фиксируется на предельном значении. В процессе вычислений такт может отойти от предельного значения и вновь стать полноценным участником процесса оптимизации.
Программы, реализующие генетический алгоритм и метод Нелдера-Мида, включены в приложение оптимизации расписания движения трамваев.
Структура приложения показана на рис. 3.
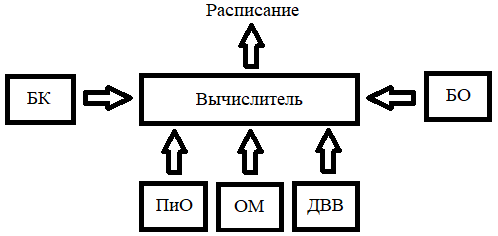
Рис. 3. Структура приложения
На рисунке использованы следующие обозначения:
Ниже приводится код, позволяющий задать параметры оптимизации, выбрать метод и критерий оптимизации и выполнить поиск оптимального расписания.
using System;
using System.IO; // StreamReader
using System.Collections.Generic; // List
using System.Windows.Forms;
namespace WindowsFormsApplicationTram
{
public partial class FormTram : Form
{
const int nCrossMax = 20; // Предельное число скрещиваний в одной эпохе
// Перестройка (restructuring) заключается в изменении числа рейсов в расписании, полученном в результате скрещивания
// В результате может получиться недопустимое расписание. Тем не менее с ним ведется работа.
// Допустимое расписание будет получено позже в результате последующих скрещиваний и корректировок
const int nRestructMax = 9; // Предельное число мутаций
const int pDI = 5, pDI2 = 9; // pDI - pDI2 - диапазон выбора величины, на которую будет уменьшено (увеличено) число рейсов расписаниия при его перестройке
const int rDecr = 8; // Параметр выбора действия из альтернативы: уменьшать или увеличивать число рейсов при перестройке (0 < rDecr < 10)
const int nDoors = 4; // Число входов в трамвай
const double pasCor = 2.2; // Коэффициент масштабирования числа пассажиров
const double kSpeed = 0.5; // Коэффициент поправки скорости
const double kSpeedTact = 1.0; // Коэффициент поправки скорости тактового расписания
const double nPAdd = 0.25; // Поправка числа пассажиров (до округления)
const int tMinPeak = 120; // Минимальное время между соседними трамваями в часы пик, с
const int tMaxPeak = 240; // Максимальное время между соседними трамваями в часы пик, с
const int tMinOth = 300; // Минимальное время между соседними трамваями в утренние и вечерние часы до и после часов пик, с
const int tMaxOth = 600; // Максимальное время между соседними трамваями в утренние и вечерние часы до и после часов пик, с
const int tMinOthDay = 240; // Минимальное время между соседними трамваями в дневные прочие часы, с
const int tMaxOthDay = 480; // Максимальное время между соседними трамваями в дневные прочие часы, с
const int tactPeak = 210; // Такт в часы пик, с
const int tactOth = 450; // Такт в утренние и вечерние прочие часы, с
const int tactOthDay = 330; // Такт в дневные прочие часы, с
const int nStops = 24; // Число остановок (без начальной)
const int tStart = 5 * 3600 + 20 * 60; // Время начала движения первого рейса, с (= 19200)
const int tEnd = 25 * 3600 + 20 * 60; // Время начала движения последнего рейса, с (= 91200 / 87600)
// Учет подхода пассажиров во время посадки
const int dtPeak = 30; // Добавка к текущему времени в часы пик, с
const int dtOth = 5; // Добавка к текущему времени в прочие часы, с
const int tInOneMin = 1; // Минимальное время посадки одного пассажира, с
const int tInOneMax = 3; // Максимальное время посадки одного пассажира, с
const int tOnStopMin = 1; // Минимальное время стоянки трамвая на остановке, с (стоит, даже если нет пассажиров)
const string fileDists = "dists.txt";
const string fileSpeeds = "speeds.txt";
const string fileParams = "params.txt"; // Читаем из файла интервал и число интервалов диаграммы прихода
const string fileStop = "stop"; // Начало имени файлов остановок
const string fileRoutes = "routes.txt"; // Файл времени прибытия трамваев маршрутов на остановки
const string fileRoutePas = "routePas.txt"; // Файл, содержащиий для каждого рейса время его начала и число перевезенных пассажиров
const string fileWaitTime = "_waitTime.txt"; // Файл, содержащиий среднее время ожидания начальных расписаний
const string fileWaitTimeOpt = "_waitTimeOpt.txt"; // Файл, содержащиий среднее время ожидания оптимизированных расписаний
const string fileBestShedI = "bestShedI.txt"; // Файл, содержащиий лучшее начальное расписание
const string fileBestShed = "bestShed.txt"; // Файл, содержащиий лучшее расписание
const string fileBestShedC = "bestShedC.txt"; // Файл, содержащиий исправленное лучшее расписание
const string textIntVal = "Интервал диаграммы прихода (мин): ";
const string textN = "Число интервалов диаграммы прихода: ";
const string textNStops = "Число остановок: ";
const string textMorn = "Утренний интервал часов пик (ч): ";
const string textEv = "Вечерний интервал часов пик (ч): ";
const string textShed0 = " - лучшего начального расписания (с): ";
const string textShed0Tact = " - начального тактового расписания (с): ";
const string textShedC = " - лучшего найденного расписания (с): ";
const string textShedRoutsN = "Начальные время ожидания и число рейсов: ";
const string textTimeSum = "Время движения по маршруту без остановок (с): ";
const string textNPasByDiags = "Нужно перевести: ";
const string textNPAll = "Всего перевезено: ";
const string textTimeStart = "Время начала движения (с): ";
const string textTimeDiagLast = "Время завершения последнего интервала диаграммы прихода (с): ";
const string textNCross = "Число скрещиваний: ";
const string textNRestruct = "Число мутаций: ";
const string textNViolations = "Число нарушений в лучшем расписании: ";
const bool diffNumberOfRoots = true; // true, если в распиисаниях популяции может быть разное число рейсов
const bool onlyEqualSheds = false;
bool tactShed; // Если true и allInitShedAreTact = false, то первое начальное расписание является тактовым
bool allInitShedAreTact = true; // Если true и tactShed = true, то все начальные расписания являются тактовыми (такты задаются с учетом часов пик)
bool improvedShed; // Если true, то генерируется улучшенное расписание (интервалы задаются с учетом часов пик)
bool simpleShed; // Если true, то генерируется простое расписание (интервалы задаются в диапазоне tMinPeak - tMaxOth)
bool turnstile; // false, если без турникета
bool doOpt; // Если false то вывод лучшего расписания начальной популяции (отмена оптимизации)
int nShedules; // Число расписаний в популяции (размер популяции)
int nCrossings; // Допустимое число попыток скрещивания в одной итерации с целью улучшения популяции
int nPAll; // Общее число перевезенных пассажиров всеми рейсами расписания
int timeInAll; // Сумммарное время посадки пассажиров в трамваи расписания, с
int timeEnd; // // Время отправления последнего рейса с последней остановки, с
int nCrossAll = 0; // Всего скрещиваний
double kOut = 1.0; // Коэффициент учета времени выхода пассажиров из травмая, равен 1 при движении с турникетами
double[] arrDist; // Массив расстояний между остановками, м
double[] arrSpeed; // Массив средних скоростей между остановками, м/с
int[] arrTMov = new int[nStops]; // Массив, каждый элемент которого - это время движения от предшествующей остановки до текущей
int[] arrTCur = new int[nStops]; // Массив времени прибытия текущего рейса на остановки маршрута, с
int[] arrTPrev = new int[nStops]; // Массив времени прибытия прежнего рейса на остановки маршрута, с
// Массив расписаний популяции. Каждый элемент массива - это список, содержащий расписание
List<int>[] arrShedules;
int[] arrWaitTime; // Массив значений среднего времени ожидания + число рейсов расписания
int[] arrNPAll; // Массив, элемент которого - это общее число перевезенных пассажиров всеми рейсами расписания
int[] arrTimeInAll; // Массив, элемент которого - это суммарное время посадки пассажиров в трамваи расписания
int[] arrTimeEnd; // Массив, элемент которого - это время прибытия последнего рейса расписания на последнюю остановку
int[,] arrDiags; // Массив диаграмм прихода
int[] arrTactPeak; // Массив тактов в часы пик, с
int[] arrTactOth; // Массив тактов в утренние и вечерние прочие часы, с
int[] arrTactOthDay; // Массив тактов в дневные прочие часы, с
int intLen; // Длина интервала диаграммы прихода, с
int N; // Число интервалов диаграммы прихода
int tLastIntEnd; // Время завершения последнего интервала диаграммы прихода, с
int timeSum; // Суммарное время движения по маршруту без остановок
int nPasByDiags; // Число перевезенных пассажиров по диаграмамм прихода (нужно перевести пассажиров)
// Начало и конец утреннего и вечернего интервалов часов пик, с
int tPeakMornStart = 0, tPeakMornEnd = 0, tPeakEvStart = 0, tPeakEvEnd = 0;
int nShedInitBest; // Лучшее начальное расписание
int seed; // Затравка датчика случайных чисел
string[] arrWaitTimeShed; // Массив отсортированных расписаний
Random rand; // Датчик случайных чисел с затравкой 24
StreamReader sR;
StreamWriter sW;
// Нелдер-Мид
int nOfTacts; // Число тактов тактового расписания
double[,] simplex;
double[] FN; // Значения функции в вершинах симплекса
double[] TW; // Значения времени ожидания в вершинах симплекса
double[] NR; // Значения числа рейсов в вершинах симплекса
List<double> LShedD = new List<double>(); // Текущее расписания
double nPAllD; // Общее число перевезенных пассажиров всеми рейсами расписания
double timeInAllD; // Сумммарное время посадки пассажиров в трамваи расписания, с
int timeLastRoutLastStop; // Время прибытия последнего рейса на последнюю остановку
public FormTram()
{
InitializeComponent();
readParams();
checkBoxTurnstile.Checked = false;
checkBoxRestruct.Checked = false;
boolValues();
readDistsSpeeds(); // Чтение файлов расстояний и средних скоростей между остановками
readDiags(); // Чтение диаграмм прихода пассажиров
//
labelShedBest0.Text = tactShed ? textShed0Tact : textShed0;
labelShedBestC.Text = textShedC;
labelShedRoutsN.Text = textShedRoutsN;
labelNPAll.Text = textNPAll;
labelTimeInAll0.Text = tactShed ? textShed0Tact : textShed0;
labelTimeInAllC.Text = textShedC;
labelTimeStart.Text = textTimeStart + tStart;
labelTimeEnd0.Text = tactShed ? textShed0Tact : textShed0;
labelTimeEndC.Text = textShedC;
tLastIntEnd = tStart + N * intLen; // Время начала движения + число интервалов диаграммы прихода * длина интервала диаграммы прихода
labelTimeDiagLast.Text = textTimeDiagLast + tLastIntEnd;
labelNCross.Text = textNCross;
labelNRestruct.Text = textNRestruct;
labelNViolations.Text = textNViolations;
}
private void readParams()
{
sR = new StreamReader((checkBoxWeekEnd.Checked ? "Выходные/" : "Будни/") + fileParams);
intLen = Convert.ToInt32(sR.ReadLine()); // Длина интервала диаграммы прихода, с
N = Convert.ToInt32(sR.ReadLine()); // Число интервалов диаграммы прихода
// Начало и конец утреннего и вечернего интервалов часов пик, с
tPeakMornStart = Convert.ToInt32(sR.ReadLine());
tPeakMornEnd = Convert.ToInt32(sR.ReadLine());
tPeakEvStart = Convert.ToInt32(sR.ReadLine());
tPeakEvEnd = Convert.ToInt32(sR.ReadLine());
sR.Close();
labelIntVal.Text = textIntVal + (intLen / 60);
labelN.Text = textN + N;
labelNStops.Text = textNStops + nStops;
labelMorn.Text = textMorn + findhM(tPeakMornStart) + " - " + findhM(tPeakMornEnd);
labelEv.Text = textEv + findhM(tPeakEvStart) + " - " + findhM(tPeakEvEnd);
}
// Возвращает строку, содержащую время в формате ЧЧ:ММ
string findhM(int time)
{
int hour = time / 3600;
int min = (time - hour * 3600) / 60;
return "" + hour + ":" + (min < 10 ? "0" : "") + min;
}
private void readDistsSpeeds()
{
string sL;
arrDist = new double[nStops]; // Массив расстояний между остановками, м
arrSpeed = new double[nStops]; // Массив средних скоростей между остановками, м/с
sR = new StreamReader(fileDists);
int k = -1;
while (!sR.EndOfStream)
{
k++;
if (k == nStops) break;
sL = sR.ReadLine();
arrDist[k] = 1000.0 * Convert.ToDouble(sL); // Переводим км в м
}
sR.Close();
sR = new StreamReader(fileSpeeds);
k = -1;
double kSpeed2 = kSpeed * (checkBoxWeekEnd.Checked ? 1.2 : 1.0);
while (!sR.EndOfStream)
{
k++;
if (k == nStops) break;
sL = sR.ReadLine();
arrSpeed[k] = (tactShed && allInitShedAreTact ? kSpeedTact : kSpeed2) * Convert.ToDouble(sL) / 3.6; // Переводим км/ч в м/с
}
sR.Close();
double t;
for (k = 0; k < nStops; k++)
{
t = arrDist[k] / arrSpeed[k];
arrTMov[k] = Convert.ToInt32(t);
}
timeSum = 0; // Суммарное время движения по маршруту без остановок
for (k = 0; k < nStops; k++) timeSum += arrTMov[k];
labelTimeSum.Text = textTimeSum + timeSum; // Суммарное время движения по маршруту без остановок, c
}
private void genPopulation()
{
int t = 0, dt = 0;
List<int> LShed;
arrShedules = new List<int>[nShedules];
arrTactPeak = new int[nShedules];
arrTactOth = new int[nShedules];
arrTactOthDay = new int[nShedules];
if (tactShed && allInitShedAreTact)
{
for (int k = 0; k < nShedules; k++)
{
arrTactPeak[k] = rand.Next(tMinPeak, tMaxPeak);
arrTactOth[k] = rand.Next(tMinOth, tMaxOth);
arrTactOthDay[k] = rand.Next(tMinOthDay, tMaxOthDay);
}
}
for (int k = 0; k < nShedules; k++)
{
LShed = new List<int>(); // Список, содержащий текущее расписание
t = tStart;
LShed.Add(t);
while (t < tEnd)
{
if (tactShed)
dt = findTact(t, k);
else if (improvedShed)
dt = find_dt(t);
else if (simpleShed)
dt = rand.Next(tMinPeak, (int)(1.5 * tMaxOth));
t += dt;
LShed.Add(Math.Min(t, tEnd));
}
arrShedules[k] = LShed;
if (simpleShed && !diffNumberOfRoots)
break;
else if (tactShed && !allInitShedAreTact)
{
tactShed = false; // Только первое расписание является тактовым
improvedShed = true; // Остальные генерируются по схеме улучшенного расписания
}
}
// Генерация популяции на основе первого расписания
if (simpleShed && !diffNumberOfRoots)
{
List<int> LShed0 = arrShedules[0];
int cnt0 = LShed0.Count - 1, t2, t3;
for (int k = 1; k < nShedules; k++)
{
LShed = new List<int>(); // Список, содержащий текущее расписание
t = tStart;
t2 = LShed0[1];
LShed.Add(tStart);
for (int m = 1; m < cnt0; m++)
{
t3 = LShed0[m + 1];
if (rand.Next(0, 1) > 0.5)
dt = -rand.Next(0, t2 - t);
else
dt = rand.Next(0, t3 - t2);
LShed.Add(t + (int)(0.75 * dt));
t = t2;
t2 = t3;
}
LShed.Add(tEnd);
arrShedules[k] = LShed;
}
}
}
// Возвращает размер такта в зависимости от периода движения
private int findTact(int t, int k)
{
if (allInitShedAreTact)
{
if (t < tPeakMornStart || t > tPeakEvEnd)
return arrTactOth[k];
else if (t > tPeakMornEnd && t < tPeakEvStart)
return arrTactOthDay[k];
else
return arrTactPeak[k];
}
else
{
if (t < tPeakMornStart || t > tPeakEvEnd)
return tactOth;
else if (t > tPeakMornEnd && t < tPeakEvStart)
return tactOthDay;
else
return tactPeak;
}
}
// Возвращает интервал между рейсам в зависимости от периода движения
private int find_dt(int t)
{
if (t < tPeakMornStart || t > tPeakEvEnd)
return rand.Next(tMinOth, tMaxOth);
else if (t > tPeakMornEnd && t < tPeakEvStart)
return rand.Next(tMinOthDay, tMaxOthDay);
else
return rand.Next(tMinPeak, tMaxPeak);
}
// Возвращает минимально допустимый интервал мажду рейсами в зависимости от типа расписания и периода движения
private int findTMin(int t)
{
if (simpleShed) return (tMinPeak + tMinOth) / 2;
if (t < tPeakMornStart || t > tPeakEvEnd)
return tMinOth;
else if (t > tPeakMornEnd && t < tPeakEvStart)
return tMinOthDay;
else
return tMinPeak;
}
// Возвращает максимально допустимый интервал мажду рейсами в зависимости от типа расписания и периода движения
private int findTMax(int t)
{
if (simpleShed) return (tMaxPeak + tMaxOth) / 2; // tMaxOth;
if (t < tPeakMornStart || t > tPeakEvEnd)
return tMaxOth;
else if (t > tPeakMornEnd && t < tPeakEvStart)
return tMaxOthDay;
else
return tMaxPeak;
}
private int calcTimeOnStop(int nP)
{
int tInOne = rand.Next(tInOneMin, tInOneMax); // // Время посадки одного пассажира, с
int tOnStop = nP * tInOne; // Сокращаем время посадки при отсутствии турникета
tOnStop = turnstile ? tOnStop : (int)((kOut * tOnStop) / nDoors);
return Math.Max(tOnStop, tOnStopMin);
}
// Симуляция расписания
private int simShed(List<int> LShed)
{
int tBT; // Время между рейсами
int tPrev; // Время предшествующего трамвая рассматриваемого рейса
int tCur; // Время текущего трамвая рассматриваемого рейса
int tWaitShed = 0; // Суммарное среднее время ожидания расписания, с
int nPRout; // Общее число пассажиров, перевезенных одним рейсом
int timeRout; // Суммарное время посадки в трамвай одного рейса, с
int nP; // Число пассажиров на остановке (все входят в трамвай)
int rout = -1;
int tOnStop; // Время пребывания трамвая на остановке
int tMin; // Минимально допустимое время между рейсами
nPAll = 0; // Общее число перевезенных пассажиров всеми рейсами расписания
timeInAll = 0; // Суммарное время посадки на трамваи расписания
foreach (int tSR in LShed) // tSR - начало движения рейса (время рейса)
{
nPRout = 0; // Общее число пассажиров, перевезенных одним рейсом
timeRout = 0; // Суммарное время посадки в трамвай одного рейса
tCur = tSR;
rout++;
if (rout == 0) // Первый рейс расписания
{
tPrev = tSR;
for (int k = 0; k < nStops; k++)
{ // Время прибытия на остановку (добавляем к текущему времени время движения между остановками)
tCur += arrTMov[k];
arrTCur[k] = tCur;
nP = findNOfPas(k, tPrev, tCur); // Число пассажиров, ожидающих трамвай
tPrev = tCur;
tOnStop = calcTimeOnStop(nP);
tCur += tOnStop; // Увеличиваем текущее время и получаем время отправления трамвая с остановки
timeRout += tOnStop;
nPRout += nP;
}
}
else // Прочие рейсы расписания
{
for (int k = 0; k < nStops; k++)
{
tCur += arrTMov[k]; // Время прибытия на остановку текущего рейса
tPrev = arrTPrev[k]; // Время прибытия на остановку прежнего рейса
tBT = tCur - tPrev; // Время между соседними рейсами
tMin = findTMin(tCur); // Минимально допустимое время между рейсами
if (tBT < 0) tCur = tPrev + tMin;
arrTCur[k] = tCur;
nP = findNOfPas(k, tPrev, tCur);
if (nP < 0) nP = 1;
tOnStop = calcTimeOnStop(nP);
tCur += tOnStop; // Увеличиваем текущее время и получаем время отправления трамвая с остановки
timeRout += tOnStop;
tWaitShed += nP * (tBT + tOnStop) / 2; // Увеличиваем время ожидания текущего рейса на время ожидания на текущей остановке
nPRout += nP;
}
}
nPAll += nPRout;
timeInAll += timeRout;
for (int k = 0; k < nStops; k++) arrTPrev[k] = arrTCur[k];
}
timeEnd = arrTCur[nStops - 1]; // Время прибытия последнего рейса на последнюю остановку (глобальная переменная)
tWaitShed = tWaitShed / nPAll + (this.radioButtonTwoCriteria.Checked ? LShed.Count : 0);
return tWaitShed; // Среднее время ожидания + число рейсов
}
private void readDiags() // Читает диаграммы прихода пасссажиров
{
int k, k2 = -1;
double pCor = checkBoxWeekEnd.Checked ? pasCor / (double)nDoors : pasCor, nPs;
string dir = (checkBoxWeekEnd.Checked ? "Выходные/" : "Будни/");
arrDiags = new int[nStops, N]; // Массив диаграмм прихода; N - число интервалов диаграммы прихода
nPasByDiags = 0;
for (k = 0; k < nStops; k++)
{
sR = new StreamReader(dir + fileStop + k + ".txt");
k2 = -1;
while (!sR.EndOfStream)
{
k2++;
nPs = pCor * Convert.ToInt32(sR.ReadLine());
arrDiags[k, k2] = (int)nPs;
nPasByDiags += (int)nPs;
}
}
labelNPas.Text = textNPasByDiags + nPasByDiags;
}
// k - номер остановки; tPrev, tCur - соответственно время предшествующего и текущего рейсов
private int findNOfPas(int k, int tPrev, int tCur)
{
// k - номер остановки; N - число интервалов диаграммы прихода
int tCur2, nP; // Правая граница времени и число пассажиров на остановке
// Время может быть в одном из трех интервалов: утреннем, вечернем или прочем
// Добавки dtPeak и dtOth введены для учета подхода пассажиров во время посадки
if (tCur >= tPeakMornStart && tCur <= tPeakMornEnd || tCur >= tPeakEvStart && tCur <= tPeakEvEnd)
tCur2 = tCur + (turnstile ? dtPeak : dtPeak / 10);
else
tCur2 = tCur + (turnstile ? dtOth : dtOth / 10);
int kT = (tCur2 - tStart) / intLen; // Номер интервала диаграмы прихода, на котором лежит tCur2
if (kT > N - 1) return -1; // Плохой рейс
int nPDiag = arrDiags[k, kT]; // Число пассажиров по диаграмме на интервале kT
int kP = (tPrev - tStart) / intLen; // Номер интервала диаграмы прихода, на котором лежит tPrev
if (kP == kT) // nPasByDiags - число пассажиров, перевозимых по диаграмме прихода (нужно перевести пассажиров)
{
nP = (int)Math.Round(1.0 * nPDiag * (tCur2 - tPrev) / (1.0 * intLen) + nPAdd);
}
else
{
int tDiag = tStart + kT * intLen; // Начало текущего интервала диаграммы
int tDiagP = tStart + (kP + 1) * intLen; // Конец предшествующего интервала диаграммы
int t = tPrev;
int kC = kP;
nP = 0;
while (tDiagP <= tDiag)
{
nP += (int)Math.Round(1.0 * arrDiags[k, kC] * (tDiagP - t) / (1.0 * intLen) + nPAdd);
kC++;
t = tDiagP;
tDiagP += intLen;
}
nP += (int)Math.Round(1.0 * nPDiag * (tCur2 - tDiag) / (1.0 * intLen) + nPAdd);
}
return nP;
//return Math.Max(nP, 1);
}
// Первая корректировка расписания; устраняем нарушение ограничения tMin
private void corrShed(List<int> LShed)
{
int tSR, tSR2, nR = LShed.Count - 2, tMin; // Не трогаем последний рейс
bool isCorr = true;
while (isCorr)
{
isCorr = false;
for (int k = 0; k < nR; k++)
{
tSR = LShed[k];
tSR2 = LShed[k + 1];
tMin = findTMin(tSR2);
if (tSR2 - tSR < tMin)
{
LShed[k + 1] = tSR + tMin; // tMin - минимально допустимое время между рейсами
isCorr = true;
}
}
}
}
// Вторая корректировка расписания; сокращаем число рейсов за счет их разрежения
private void corrShed2(List<int> LShed)
{
int tSR, nR, nDelMax = 15, nDel = 0, tMax;
bool isDel = true;
while (isDel && nDel < nDelMax)
{
isDel = false;
nR = LShed.Count - 2;
for (int k = 0; k < nR; k++)
{
tSR = LShed[k];
tMax = findTMax(tSR);
if (LShed[k + 2] - tSR < 0.5 * tMax)
{
tSR = LShed[k + 1];
LShed.RemoveAt(k + 1); // Сокращаем число рейсов за счет разрежения рейсов
if (checkShed(LShed, false) > 0)
LShed.Insert(k + 1, tSR);
else
{
isDel = true;
nDel++;
break;
}
}
}
}
}
// Третья корректировка расписания; устраняем нарушение tMax
private void corrShed3(List<int> LShed)
{
int tSR, tSR2, nInsMax = 50, nIns = 0, tMax, nR = LShed.Count - 3; // Время последнего рейса не меняем
bool isCorr = true, isIns = true;
while (isCorr)
{
isCorr = false;
for (int k = 0; k < nR; k++)
{
tSR = LShed[k];
tSR2 = LShed[k + 1];
tMax = findTMax(tSR2);
if (tSR2 - tSR > tMax) // tMax - максимально допустимый интервал между соседними рейсами
{
LShed[k + 1] = tSR + tMax;
isCorr = true;
}
}
}
// Контроль последнего интервала
while (isIns && nIns < nInsMax)
{
isIns = false;
tSR = LShed[nR];
if (LShed[nR + 1] - tSR > (simpleShed ? (tMaxPeak + tMaxOth) / 2 : tMaxOth)) // tMaxOth - максимально допустимый интервал между рейсами утром и вечером до и после часов пик
{
LShed.Insert(nR + 1, tSR + 3 * (simpleShed ? (tMaxPeak + tMaxOth) / 2 : tMaxOth) / 4); // Вставляем рейс
nIns++;
isIns = true;
}
nR++;
}
}
private int checkShed(List<int> LShed, bool writeToFile) // Проверка расписания
{
int nLess = 0, nMore = 0, nR = LShed.Count - 2;
int errtMin = int.MinValue, errtMax = int.MinValue;
int kMin = 0, kMax = 0, tMin, tMax, dt, tSR, tSR2;
for (int k = 0; k < nR; k++)
{
tSR = LShed[k];
tSR2 = LShed[k + 1];
tMin = findTMin(tSR2);
tMax = findTMax(tSR2);
dt = tSR2 - tSR;
if (dt < tMin)
{
nLess++;
if (tMin - dt > errtMin)
{
kMin = k + 1;
errtMin = tMin - dt;
}
}
if (dt > tMax)
{
nMore++;
if (dt - tMax > errtMax)
{
kMax = k + 1;
errtMax = dt - tMax;
}
}
}
if (writeToFile)
{
if (nLess > 0)
{
sW.WriteLine("Число нарушений нижнего интервала: " + nLess);
sW.WriteLine("Величина наибольшего нарушения, с: " + errtMin + ". Рейс: " + (kMin + 1));
}
if (nMore > 0)
{
sW.WriteLine("Число нарушений верхнего интервала: " + nMore);
sW.WriteLine("Величина наибольшего нарушения, с: " + errtMax + ". Рейс: " + (kMax + 1));
}
}
return nLess + nMore;
}
// Скрещивание пар отобранных расписаний
private bool crossing()
{
string shed, shedS2, shedB, shedW;
int nShed, nShed2, nShedB, nShedW, m, nR, tSR, nR2, tWaitShedC;
List<int> LShed, LShed2, LShedC;
shedB = arrWaitTimeShed[0]; // Лучшее расписание
nShedB = Convert.ToInt32(shedB.Substring(4));
// nCrossings - допустимое число попыток скрещивания в одной итерации с целью улучшения популяции
for (int k = 0; k < nCrossings - 1; k++)
{
shed = arrWaitTimeShed[k];
nShed = Convert.ToInt32(shed.Substring(4));
LShed = arrShedules[nShed];
nR = LShed.Count;
for (int k2 = 1; k2 < nShedules; k2++)
{
shedS2 = arrWaitTimeShed[k2];
nShed2 = Convert.ToInt32(shedS2.Substring(4));
LShed2 = arrShedules[nShed2];
nR2 = LShed2.Count;
if (onlyEqualSheds && nR != nR2) continue;
LShedC = new List<int>(); // Результат скрещивания
for (m = 0; m < nR; m++) LShedC.Add(LShed[m]);
for (m = 1; m < nR; m++)
{
tSR = LShed[m]; // tSR - начало движения рейса
if (m < nR2) LShedC[m] = (tSR + LShed2[m]) / 2;
if (checkShed(LShedC, false) > 0) LShedC[m] = tSR;
}
LShedC[nR - 1] = tEnd;
corrShed(LShedC); // Устраняем нарушение ограничения tMin
corrShed2(LShedC); // Сокращаем число рейсов за счет разрежения рейсов
corrShed3(LShedC); // Устраняем нарушение tMax
tWaitShedC = simShed(LShedC); // Симуляция расписания
if (tWaitShedC < arrWaitTime[nShedB]) // nShedB - номер текущего лучшего расписания
{
shedW = arrWaitTimeShed[nShedules - 1]; // Худшее расписание
nShedW = Convert.ToInt32(shedW.Substring(4));
arrShedules[nShedW] = LShedC;
arrWaitTime[nShedW] = tWaitShedC;
arrNPAll[nShedW] = nPAll;
arrTimeInAll[nShedW] = timeInAll;
arrTimeEnd[nShedW] = timeEnd; // Время отправления последнего рейса с последней остановки (глобальная переменная)
return true;
}
}
}
return false;
}
private void sortSheds()
{
for (int k = 0; k < nShedules; k++) arrWaitTimeShed[k] = "" + arrWaitTime[k] + "-" + k;
Array.Sort(arrWaitTimeShed);
}
// Находит время ожидания для вывода на экран и файл
private string findTWaitShed(int tWR, int nR)
{
int tW = (radioButtonTwoCriteria.Checked ? tWR - nR : tWR);
return "" + tW + " / " + nR + ". Время ожидания + число рейсов: " + (tW + nR);
}
private void mutation(int nShed) // Мутация расписания
{
List<int> LShed; // Текущее расписание
LShed = arrShedules[nShed];
// Получаем случайное число k от pDI до pDI2
// Получаем случайное число k2 от 0 до 10
// Если k2 < rDecr, то уменьшаем число рейсов текущего лучшего расписания на k%,
// в противном случае увеличиваем число рейсов на те же k%
int k = rand.Next(pDI, pDI2);
int k2 = rand.Next(0, 10);
int nR = LShed.Count - 1; // Число рейсов
int dt, dt2, rToDel = 0, rToIns = 0, tSR;
if (k2 < rDecr) // Удаляем рейсы
{
for (int i = 0; i < k; i++)
{
// Находим рейс вне часов пик, для которого tSubs - tPrev минимально, где
// tPrev - время предшествующего рейса
// tSubs - время последующего рейса (subsequent)
dt = int.MaxValue;
for (int j = 1; j < nR; j++)
{
tSR = LShed[j];
if (tSR < tPeakMornStart || tSR > tPeakMornEnd && tSR < tPeakEvStart || tSR > tPeakEvEnd) // Время рейса вне часов пик
{
dt2 = LShed[j + 1] - LShed[j - 1]; // tSubs - tPrev
if (dt2 < dt)
{
rToDel = j;
dt = dt2;
}
}
}
tSR = LShed[rToDel];
LShed.RemoveAt(rToDel);
if (checkShed(LShed, false) > 0)
LShed.Insert(rToDel, tSR);
else
nR--;
}
}
else // Добаляем рейсы
{
for (int i = 0; i < k; i++)
{
// Находим рейс вне часов пик, для которого tSubs - tSR максимально, где
// tSR - время текущего рейса
// tSubs - время последующего рейса (subsequent)
dt = int.MinValue;
for (int j = 1; j < nR; j++)
{
tSR = LShed[j];
if (tSR < tPeakMornStart || tSR > tPeakMornEnd && tSR < tPeakEvStart || tSR > tPeakEvEnd) // Время рейса вне часов пик
{
dt2 = LShed[j + 1] - tSR; // tSubs - tSR
if (dt2 > dt)
{
rToIns = j;
dt = dt2;
}
}
}
LShed.Insert(rToIns, (LShed[rToIns - 1] + LShed[rToIns]) / 2);
nR++;
}
}
}
private void writeResult(List<int> LShed, StreamWriter sW)
{
int nV = checkShed(LShed, true); // Число нарушений в расписании LShed
labelNViolations.Text = textNViolations + nV;
sW.WriteLine("Расписание:");
int m = 0, tPrev = LShed[0], tMin, tMax, dt;
string add = "", sPeak = ". Часы пик";
foreach (int tSR in LShed)
{
tMin = findTMin(tSR);
tMax = findTMax(tSR);
if (m > 1)
{
dt = tSR - tPrev;
if (dt > tMax)
add = " dt > tMax на " + (dt - tMax) + "; dt = " + dt + "; tMax = " + tMax;
else if (dt < tMin)
add = " dt < tMin на " + (tMin - dt) + "; dt = " + dt + "; tMin = " + tMin;
else
add = "";
}
m++;
sW.WriteLine("" + tSR + " - " + m + add + (tSR > tPeakMornStart && tSR < tPeakMornEnd || tSR > tPeakEvStart && tSR < tPeakEvEnd ? sPeak : ""));
tPrev = tSR;
}
sW.Close();
}
private void putWaitTime(string fileNm, string s)
{
int nShed, tW, nR;
List<int> LShed;
sW = new StreamWriter(fileNm);
sW.WriteLine("Время ожидания и число рейсов " + s);
for (int k = 0; k < nShedules; k++)
{
nShed = Convert.ToInt32(arrWaitTimeShed[k].Substring(4));
tW = arrWaitTime[nShed];
LShed = arrShedules[nShed];
nR = LShed.Count;
sW.WriteLine("" + (radioButtonTwoCriteria.Checked ? tW - nR : tW) + "/" + LShed.Count + "; число нарушений: " + checkShed(LShed, false));
}
sW.Close();
}
private void buttonGo_Click(object sender, EventArgs e)
{
List<int> LShed, LShedInitBest; // Текущее и лучшее начальное расписания
int nCross, nShed = 0, nRInitBest, tWInitBest, timeInAllInitBest, timeEndInitBest, nPAllInitBest, nR, seed, tW;
string routsN = ""; // Строка с временем ожидания и числа рейсов расписаний начальной популяции
boolValues();
seed = (int)numericUpDownSeed.Value;
rand = new Random(seed); // Датчик случайных чисел с затравкой seed
// Инициализация
arrWaitTime = new int[nShedules];
arrNPAll = new int[nShedules];
arrTimeInAll = new int[nShedules];
arrTimeEnd = new int[nShedules];
genPopulation(); // Генерация начальной популяциии расписаний
for (nShed = 0; nShed < nShedules; nShed++) // Симуляция начальной популяции
{
LShed = arrShedules[nShed]; // Текущее расписание
arrWaitTime[nShed] = simShed(LShed); // Симуляция расписания; минимизируем число рейсов и/или среднее время ожидания
arrNPAll[nShed] = nPAll;
arrTimeInAll[nShed] = timeInAll;
arrTimeEnd[nShed] = timeEnd; // Время отправления последнего рейса с последней остановки (глобальная переменная)
if (nShed == 0) labelNPAll.Text = textNPAll + nPAll;
}
arrWaitTimeShed = new string[nShedules];
sortSheds();
for (int k = 0; k < nShedules; k++) // Симуляция начальной популяции
{
nShed = Convert.ToInt32(arrWaitTimeShed[k].Substring(4));
tW = arrWaitTime[nShed];
nR = arrShedules[nShed].Count; // Число рейсов в расписании
routsN = routsN + (radioButtonTwoCriteria.Checked ? tW - nR : tW) + "/" + nR + "; ";
}
labelShedRoutsN.Text = textShedRoutsN + routsN;
bool rbt = radioButtonTactShed.Checked && !allInitShedAreTact;
nShedInitBest = rbt ? 0 : Convert.ToInt32(arrWaitTimeShed[0].Substring(4));
LShedInitBest = arrShedules[nShedInitBest];
nRInitBest = LShedInitBest.Count;
nPAllInitBest = arrNPAll[nShedInitBest];
tWInitBest = arrWaitTime[nShedInitBest];
timeInAllInitBest = arrTimeInAll[nShedInitBest]; // Суммарное время посадки лучшего начального расписания
timeEndInitBest = arrTimeEnd[nShedInitBest]; // Время прибытия последнего рейса на конечную остановку лучшего начального расписания
labelShedBest0.Text = (rbt ? textShed0Tact : textShed0) + findTWaitShed(tWInitBest, nRInitBest);
labelTimeInAll0.Text = (rbt ? textShed0Tact : textShed0) + timeInAllInitBest;
labelTimeEnd0.Text = (rbt ? textShed0Tact : textShed0) + timeEndInitBest;
putWaitTime(fileWaitTime, "начальных расписаний");
sW = new StreamWriter(fileBestShedI);
sW.WriteLine("Начальная популяция: " + (radioButtonTactShed.Checked ? "на базе тактового" : (simpleShed ? "простая" : "улучшенная")));
sW.WriteLine("Движение " + (checkBoxTurnstile.Checked ? "с турникетом" : "без турникета"));
sW.WriteLine("Лучшее начальное расписание:");
sW.WriteLine(" - среднее время ожидания: " + findTWaitShed(tWInitBest, nRInitBest));
sW.WriteLine(" - число рейсов: " + nRInitBest);
writeResult(LShedInitBest, sW);
sW.Close();
// Оптимизация
int nRestruct = 0;
nCrossAll = 0;
if (doOpt)
{
if (checkBoxRestruct.Checked && diffNumberOfRoots)
{
while (nRestruct < nRestructMax)
{
nRestruct++;
for (int k = 1; k < nCrossings; k++)
{
nShed = Convert.ToInt32(arrWaitTimeShed[1].Substring(4)); // Второе по качеству расписание
mutation(nShed);
LShed = arrShedules[nShed]; // Текущее расписание
arrWaitTime[nShed] = simShed(LShed); // Симуляция расписания после мутации
arrNPAll[nShed] = nPAll;
arrTimeInAll[nShed] = timeInAll;
arrTimeEnd[nShed] = timeEnd; // Время отправления последнего рейса с последней остановки (глобальная переменная)
}
sortSheds();
nCross = 0; // Число скрещиваний после мутации
while (crossing() && nCross < 10 * nCrossMax) // Скрещивание лучших расписаний
{
nCross++;
nCrossAll++;
sortSheds();
}
}
}
else
{
while (crossing() && nCrossAll < nCrossMax) // Скрещивание лучших расписаний
{
nCrossAll++;
sortSheds();
}
}
putWaitTime(fileWaitTimeOpt, "оптимизированных расписаний");
}
nShed = Convert.ToInt32(arrWaitTimeShed[0].Substring(4)); // Лучшее расписание
LShed = arrShedules[nShed]; // Лучшее расписание
nR = LShed.Count;
nRestruct = (checkBoxRestruct.Checked && diffNumberOfRoots ? nRestructMax : 0); // Число мутаций
labelShedBestC.Text = textShedC + findTWaitShed(arrWaitTime[nShed], nR);
labelTimeInAllC.Text = textShedC + arrTimeInAll[nShed];
labelTimeEndC.Text = textShedC + arrTimeEnd[nShed];
labelNCross.Text = textNCross + nCrossAll;
labelNRestruct.Text = textNRestruct + nRestruct;
sW = new StreamWriter(fileBestShed);
sW.WriteLine("Начальная популяция: " + (radioButtonTactShed.Checked ? "на базе тактового" : (simpleShed ? "простая" : "улучшенная")));
sW.WriteLine("Движение " + (checkBoxTurnstile.Checked ? "с турникетом" : "без турникета"));
sW.WriteLine("Число скрещиваний: " + nCrossAll);
sW.WriteLine("Число мутаций: " + nRestruct);
sW.WriteLine("Среднее время ожидания:");
sW.WriteLine("- лучшего начального расписания: " + findTWaitShed(tWInitBest, nRInitBest));
sW.WriteLine("- лучшего расписания: " + findTWaitShed(arrWaitTime[nShed], nR));
sW.WriteLine("Число рейсов:");
sW.WriteLine("- лучшего начального расписания: " + nRInitBest);
sW.WriteLine("- лучшего расписания: " + nR);
sW.WriteLine("Нужно перевезти пассажиров: " + nPasByDiags);
sW.WriteLine("Перевезено пассажиров:");
sW.WriteLine("- лучшим начальным расписанием: " + nPAllInitBest);
sW.WriteLine("- лучшим расписанием: " + arrNPAll[nShed]);
sW.WriteLine("Суммарное время посадки: ");
sW.WriteLine("- лучшго начального расписания: " + timeInAllInitBest);
sW.WriteLine("- лучшего расписания: " + arrTimeInAll[nShed]);
sW.WriteLine("Время прибытия последнего рейса на последнюю остановку:");
sW.WriteLine("- лучшего начального расписания: " + timeEndInitBest);
sW.WriteLine("- лучшего расписания: " + arrTimeEnd[nShed]);
sW.WriteLine("Время завершения последнего интервала: " + tLastIntEnd);
writeResult(LShed, sW);
}
private void boolValues()
{
tactShed = radioButtonTactShed.Checked; // Если true, то генерируются тактовые начальные расписания (такты задаются с учетом часов пик)
improvedShed = radioButtonImprovedShed.Checked; // Если true, то генерируется улучшенное расписание (интервалы задаются с учетом часов пик)
simpleShed = radioButtonSimpleShed.Checked; // Если true, то генерируется простое расписание (интервалы задаются в диапазоне tMinPeak, tMaxOth)
turnstile = checkBoxTurnstile.Checked;
doOpt = checkBoxDoOpt.Checked; // Если false то вывод лучшего расписания начальной популяции (отмена оптимизации)
nShedules = Convert.ToInt32(numericUpDownNShedules.Value); // Число расписаний в популяции (размер популяции)
nCrossings = 10; // Допустимое число попыток скрещивания в одной итерации с целью улучшения популяции
labelShedBest0.Text = tactShed ? textShed0Tact : textShed0;
labelTimeInAll0.Text = tactShed ? textShed0Tact : textShed0;
labelTimeEnd0.Text = tactShed ? textShed0Tact : textShed0;
}
private void buttonChange_Click(object sender, EventArgs e)
{
List<int> LShed = new List<int>(); // Расписание
sR = new StreamReader(fileBestShed);
int k, nR, tW, nR0 = 0;
string s = "";
rand = new Random(); // Датчик случайных чисел с затравкой seed
boolValues();
for (k = 0; k < 50; k++)
{
if (sR.EndOfStream)
{
MessageBox.Show("Плохой файл " + fileBestShed);
return;
}
if (sR.ReadLine() == "Расписание:") break;
}
while (!sR.EndOfStream)
{
s = sR.ReadLine();
LShed.Add(Convert.ToInt32(s.Substring(0, 5)));
nR0++;
}
sR.Close();
corrShed(LShed); // Устраняем нарушение ограничения tMin
corrShed2(LShed); // Сокращаем число рейсов за счет разрежения рейсов
corrShed3(LShed); // Устраняем нарушение tMax
tW = simShed(LShed); // Среднее время ожидания расписания
nR = LShed.Count;
sW = new StreamWriter(fileBestShedC);
sW.WriteLine("После правки:");
sW.WriteLine(" - перевезено пассажиров: " + nPAll);
sW.WriteLine(" - среднее время ожидания: " + findTWaitShed(tW, nR));
sW.WriteLine(" - число рейсов: " + nR);
sW.WriteLine("Число рейсов до правки: " + nR0);
writeResult(LShed, sW);
sW.Close();
labelNPas.Text = textNPasByDiags + nPasByDiags;
labelNPAll.Text = textNPAll + nPAll;
labelShedBestC.Text = textShedC + findTWaitShed(tW, nR);
labelTimeInAllC.Text = textShedC + timeInAll;
labelTimeEndC.Text = textShedC + timeEnd;
labelShedRoutsN.Text = textShedRoutsN + nR;
}
private void radioButtonTactShed_CheckedChanged(object sender, EventArgs e)
{
boolValues();
readDistsSpeeds();
}
private void buttonClose_Click(object sender, EventArgs e)
{
Close();
}
private double F(double[] X, int NP, int i) // Функциия составления и симуляции расписания
{
double t = tStart, dt = 0;
LShedD = new List<double>();
LShedD.Add(t);
while (t < tEnd)
{
if (NP == 2)
{
if (t < tPeakMornStart || t > tPeakEvEnd || t > tPeakMornEnd && t < tPeakEvStart)
dt = X[0]; // Такт для прочих часов
else
dt = X[1]; // Такт для часов пик
}
else if (NP == 3)
{
if (t < tPeakMornStart || t > tPeakEvEnd)
dt = X[0]; // Такт до утренних и после вечерних часов пик
else if (t > tPeakMornEnd && t < tPeakEvStart)
dt = X[2]; // Такт для дневных непиковых часов
else
dt = X[1]; // Такт для часов пик
}
else if (NP == 4)
{
if (t < tPeakMornStart || t > tPeakEvEnd)
dt = X[0]; // Такт до утренних и после вечерних часов пик
else if (t > tPeakMornEnd && t <= tPeakEvStart)
dt = X[2]; // Такт для дневных непиковых часов
else if (t <= tPeakMornEnd)
dt = X[1]; // Такт для утренних часов пик
else
dt = X[3]; // Такт для вечерних часов пик
}
else if (NP == 5)
{
if (t < tPeakMornStart)
dt = X[0]; // Такт до утренних часов пик
else if (t > tPeakMornEnd && t <= tPeakEvStart)
dt = X[2]; // Такт для дневных непиковых часов
else if (t > tPeakEvEnd)
dt = X[4]; // Такт для вечерних непиковых часов
else if (t <= tPeakMornEnd)
dt = X[1]; // Такт для утренних часов пик
else
dt = X[3]; // Такт для вечерних часов пик
}
t += dt;
LShedD.Add(Math.Min(t, tEnd));
}
double C = simShedD(LShedD);
NR[i] = LShedD.Count;
TW[i] = C - NR[i];
return C;
}
// Создает из точки X регулярный симплекс с длиной ребра L и с NP + 1 вершиной
// Формирует массив FN значений оптимизируемой функции F в вершинах симплекса
private void makeSimplex(double[] X, double L, int NP, bool first)
{
double qn, q2, r1, r2;
int i, j;
qn = Math.Sqrt(1.0 + NP) - 1.0;
q2 = L / Math.Sqrt(2.0) * (double)NP;
r1 = q2 * (qn + (double)NP);
r2 = q2 * qn;
for (i = 0; i < NP; i++) simplex[i, 0] = X[i];
for (i = 1; i < NP + 1; i++)
for (j = 0; j < NP; j++)
simplex[j, i] = X[j] + r2;
for (i = 1; i < NP + 1; i++) simplex[i - 1, i] = simplex[i - 1, i] - r2 + r1;
for (i = 0; i < NP + 1; i++)
{
for (j = 0; j < NP; j++) X[j] = simplex[j, i];
//sW.WriteLine("Вершины начального симплекса:");
//for (j = 0; j < NP; j++) sW.WriteLine(X[j]);
FN[i] = F(X, NP, i); // Значения функции в вершинах начального симплекса
}
if (first)
{
sW.WriteLine("Значения функции в вершинах начального симплекса:");
for (i = 0; i < NP + 1; i++) sW.WriteLine("" + FN[i] + " = (" + TW[i] + " + " + NR[i] + ")");
sW.WriteLine("Значения времени ожидания в вершинах начального симплекса:");
for (i = 0; i < NP + 1; i++) sW.WriteLine(TW[i]);
sW.WriteLine("Значения числа рейсов в вершинах начального симплекса:");
for (i = 0; i < NP + 1; i++) sW.WriteLine(NR[i]);
}
}
private double[] center_of_gravity(int k, int NP) // Центр тяжести симплекса
{
int i, j;
double s;
double[] xc = new double[NP];
for (i = 0; i < NP; i++)
{
s = 0;
for (j = 0; j < NP + 1; j++) s += simplex[i, j];
xc[i] = s;
}
for (i = 0; i < NP; i++) xc[i] = (xc[i] - simplex[i, k]) / (double)NP;
return xc;
}
private void reflection(int k, double cR, int NP) // Отражение вершины с номером k относительно центра тяжести
{
double[] xc = center_of_gravity(k, NP); // cR – коэффициент отражения
for (int i = 0; i < NP; i++) simplex[i, k] = (1.0 + cR) * xc[i] - simplex[i, k];
// Контроль ограничения
double s = 0.75 * tMinPeak;
for (int i = 0; i < NP; i++) if (simplex[i, k] < s) simplex[i, k] = s;
s = 1.01 * tMaxOth;
for (int i = 0; i < NP; i++) if (simplex[i, k] > s) simplex[i, k] = s;
}
private void reduction(int k, double gamma, int NP) // Редукция симплекса к вершине k
{
int i, j; // gamma – коэффициент редукции
double[] xk = new double[NP];
for (i = 0; i < NP; i++) xk[i] = simplex[i, k];
for (j = 0; j < NP; j++)
for (i = 0; i < NP; i++)
simplex[i, j] = xk[i] + gamma * (simplex[i, j] - xk[i]);
for (i = 0; i < NP; i++) simplex[i, k] = xk[i]; // Восстанавливаем симплекс в вершине k
// Контроль ограничения
double s = 0.75 * tMinPeak;
for (j = 0; j < NP; j++)
for (i = 0; i < NP; i++)
if (simplex[i, j] < s) simplex[i, j] = s;
}
private void shrinking_expansion(int k, double alpha_beta, int NP) // Сжатие/растяжение симплекса. alpha_beta – коэффициент растяжения/сжатия
{
double[] xc = center_of_gravity(k, NP);
for (int i = 0; i < NP; i++)
simplex[i, k] = xc[i] + alpha_beta * (simplex[i, k] - xc[i]);
double s;
// Контроль ограничения
if (alpha_beta < 1)
{
s = 0.75 * tMinPeak;
for (int j = 0; j < NP; j++)
for (int i = 0; i < NP; i++)
if (simplex[i, j] < s) simplex[i, j] = s;
}
else
{
s = 1.01 * tMaxOth;
for (int j = 0; j < NP; j++)
for (int i = 0; i < NP; i++)
if (simplex[i, j] > s) simplex[i, j] = s;
}
}
private double findL(double[] X2, int NP) // Длиина ребра симплекса
{
double L = 0;
for (int i = 0; i < NP; i++) L += X2[i] * X2[i];
return Math.Sqrt(L);
}
private double minval(double[] F, int N1, ref int imi) // Минимальный элемент массива и его индекс
{
double fmi = double.MaxValue, f;
for (int i = 0; i < N1; i++)
{
f = F[i];
if (f < fmi)
{
fmi = f;
imi = i;
}
}
return fmi;
}
private double maxval(double[] F, int N1, ref int ima) // Максимальный элемент массива и его индекс
{
double fma = double.MinValue, f;
for (int i = 0; i < N1; i++)
{
f = F[i];
if (f > fma)
{
fma = f;
ima = i;
}
}
return fma;
}
private void simplexRestore(int NP) // Восстанавление симплекса
{
int i, imi = -1, imi2 = -1;
double fmi, fmi2 = double.MaxValue, f;
double[] X = new double[NP], X2 = new double[NP];
fmi = minval(FN, NP + 1, ref imi);
for (i = 0; i < NP + 1; i++)
{
f = FN[i];
if (f != fmi && f < fmi2)
{
fmi2 = f;
imi2 = i;
}
}
if (imi2 == -1) imi2 = 1 - imi;
for (i = 0; i < NP; i++)
{
X[i] = simplex[i, imi];
X2[i] = simplex[i, imi] - simplex[i, imi2];
}
makeSimplex(X, findL(X2, NP), NP, false);
}
private bool notStopYet(double L_thres, int NP) // Возвращает true, если длина хотя бы одного ребра симплекса превышает L_thres, или false - в противном случае
{
int i, j, k;
double[] X = new double[NP], X2 = new double[NP];
for (i = 0; i < NP; i++)
{
for (j = 0; j < NP; j++) X[j] = simplex[j, i];
for (j = i + 1; j < NP + 1; j++)
{
for (k = 0; k < NP; k++) X2[k] = X[k] - simplex[k, j];
if (findL(X2, NP) > L_thres) return true;
}
}
return false;
}
// k - номер остановки; tCur - время текущего рейса
private double findNOfPasD(int k, double T, double tCur, int rout)
{
double tCur2, nP; // Текущее время с учетом времени подхода и число пассажиров на остановке
// Время может быть в одном из трех интервалов: утреннем, вечернем или прочем
// Добавки dtPeak и dtOth введены для учета подхода пассажиров во время посадки
if (tCur >= tPeakMornStart && tCur <= tPeakMornEnd || tCur >= tPeakEvStart && tCur <= tPeakEvEnd)
tCur2 = tCur + (turnstile ? dtPeak : dtPeak / 10.0);
else
tCur2 = tCur + (turnstile ? dtOth : dtOth / 10.0);
// Номер интервала диаграмы прихода, на котором лежит tCur2
// tStart - время начала движения (первого рейса)
int kT = (int)((tCur2 - tStart) / (double)intLen);
if (kT > N - 1) // N - число интервалов диаграммы прихода
{
kT = N - 1;
}
if (kT < 0)
{
kT = 0;
}
double nPDiag = arrDiags[k, kT]; // Число пассажиров по диаграмме на интервале kT
double tPrev = tCur - T;
// Номер интервала диаграмы прихода, на котором лежит время tPrev прихода предыдущего рейса
int kP = (int)((tPrev - tStart) / (double)intLen);
if (kP > kT)
{
kP = kT;
}
if (kP < 0)
{
kP = 0;
}
if (kP == kT) // nPasByDiags - число пассажиров, перевозимых по диаграмме прихода (столько пассажиров нужно перевести)
{
nP = nPDiag * (tCur2 - tPrev) / (double)intLen;
}
else
{
double tDiag = tStart + kT * intLen; // Начало текущего интервала диаграммы
double tDiagP = tStart + (kP + 1) * intLen; // Конец предшествующего интервала диаграммы
double t = tPrev;
int kC = kP;
nP = 0;
while (tDiagP <= tDiag)
{
nP += (double)arrDiags[k, kC] * (tDiagP - t) / (double)intLen;
kC++;
t = tDiagP;
tDiagP += intLen;
}
nP += nPDiag * (tCur2 - tDiag) / (double)intLen;
}
return nP;
}
// Симуляция расписания
private double simShedD(List<double> LShedD)
{
double tCur = 0; // Время текущего трамвая рассматриваемого рейса
double tWaitShed = 0; // Суммарное среднее время ожидания расписания, с
double nPRout; // Общее число пассажиров, перевезенных одним рейсом
double timeRout; // Суммарное время посадки в трамвай одного рейса, с
double nP; // Число пассажиров на остановке (все входят в трамвай)
int rout = -1;
double tOnStop; // Время пребывания трамвая на остановке
double T = LShedD[1] - LShedD[0]; // Размер такта; разный для разных рейсов
nPAllD = 0; // Общее число перевезенных пассажиров всеми рейсами расписания
timeInAllD = 0; // Суммарное время посадки на трамваи расписания
int m = -1;
foreach (double tSR in LShedD) // tSR - начало движения рейса (время рейса)
{
m++;
nPRout = 0; // Общее число пассажиров, перевезенных одним рейсом
timeRout = 0; // Суммарное время посадки в трамвай одного рейса
tCur = tSR;
rout++;
if (rout == 0) // Первый рейс расписания
{
for (int k = 0; k < nStops; k++)
{ // Время прибытия на остановку (добавляем к текущему времени время движения между остановками)
if (T < tMinPeak)
{
sW.WriteLine("T < tMinPeak (0)");
T = tactOthDay;
}
tCur += T;
nP = findNOfPasD(k, T, tCur, rout); // Число пассажиров, ожидающих трамвай
tOnStop = calcTimeOnStopD(nP);
timeRout += tOnStop;
nPRout += nP;
tWaitShed += nP * T / 2.0; // Увеличиваем время ожидания текущего рейса на среднее время ожидания на текущей остановке
}
}
else // Прочие рейсы расписания
{
T = tSR - LShedD[m - 1];
for (int k = 0; k < nStops; k++)
{
tCur += T; // Время прибытия на остановку текущего рейса
if (tCur > tLastIntEnd)
{
tCur -= T;
break;
}
nP = findNOfPasD(k, T, tCur, rout);
if (nP < 0)
{
sW.WriteLine("nP < 0. k = " + k + ". rout = " + rout);
nP = 1;
}
tOnStop = calcTimeOnStopD(nP);
timeRout += tOnStop;
tWaitShed += nP * T / 2.0; // Увеличиваем время ожидания текущего рейса на среднее время ожидания на текущей остановке
nPRout += nP;
}
}
nPAllD += nPRout;
timeInAllD += timeRout;
}
timeLastRoutLastStop = (int)tCur;
if (radioButtonTwoCriteria.Checked)
tWaitShed = tWaitShed / nPAllD + LShedD.Count;
else if (radioButtonOnlyNR.Checked)
tWaitShed = LShedD.Count;
else
tWaitShed = tWaitShed / nPAllD;
return tWaitShed; // Среднее время ожидания + число рейсов, если radioButtonTwoCriteria.Checked = true
}
private double calcTimeOnStopD(double nP)
{
double tInOne = ((double)tInOneMin + (double)tInOneMax) / 2; // Время посадки одного пассажира, с
double tOnStop = nP * tInOne;
tOnStop = turnstile ? tOnStop : kOut * (tOnStop / nDoors); // Сокращаем время посадки при отсутствии турникета
return Math.Max(tOnStop, tOnStopMin);
}
private void checkBoxWeekEnd_CheckedChanged(object sender, EventArgs e)
{
readParams();
readDistsSpeeds(); // Чтение файлов расстояний и средних скоростей между остановками
readDiags();
}
// Выполняет поиск экстремума (минимума) функции F
private void nelMead(ref double[] X, int NP, double L, double L_thres, double cR, double alpha, double beta, double gamma, int jMx, int kr_todo)
{
int i, j2, imi = -1, ima = -1, kr = 0; // kr - число шагов после восстановления симплекса
int nIt = 0; // Число шагов алгоритма
double[] X2 = new double[NP], X_R = new double[NP];
double Fmi, Fma, F_R, F_S, F_E;
double TW_R, NR_R, TW_S, NR_S, TW_E, NR_E;
makeSimplex(X, L, NP, true);
while (notStopYet(L_thres, NP) && nIt < jMx)
{
nIt++; // Число итераций
kr++;
if (kr == kr_todo)
{
kr = 0;
simplexRestore(NP); // Восстановление симплекса
}
Fmi = minval(FN, NP + 1, ref imi);
Fma = maxval(FN, NP + 1, ref ima); // ima - Номер отражаемой вершины
for (i = 0; i < NP; i++) X[i] = simplex[i, ima];
reflection(ima, cR, NP); // Отражение
for (i = 0; i < NP; i++) X_R[i] = simplex[i, ima];
F_R = F(X_R, NP, ima); // Значение функции в вершине ima симплекса после отражения
TW_R = TW[ima];
NR_R = NR[ima];
if (F_R > Fma)
{
shrinking_expansion(ima, beta, NP); // Сжатие
for (i = 0; i < NP; i++) X2[i] = simplex[i, ima];
F_S = F(X2, NP, ima); // Значение функции в вершине ima симплекса после его сжатия
TW_S = TW[ima];
NR_S = NR[ima];
if (F_S > Fma)
{
for (i = 0; i < NP; i++) simplex[i, ima] = X[i];
reduction(ima, gamma, NP); // Редукция
for (i = 0; i < NP + 1; i++)
{
if (i == ima) continue;
for (j2 = 0; j2 < NP; j2++) X2[j2] = simplex[j2, i];
// Значения функций в вершинах симплекса после редукции. В вершине ima значение функции сохраняется
FN[i] = F(X2, NP, i);
}
}
else
FN[ima] = F_S;
TW[ima] = TW_S;
NR[ima] = NR_S;
}
else if (F_R < Fmi)
{
shrinking_expansion(ima, alpha, NP); // Растяжение
for (j2 = 0; j2 < NP; j2++) X2[j2] = simplex[j2, ima];
F_E = F(X2, NP, ima); // Значение функции в вершине ima симплекса после его растяжения
TW_E = TW[ima];
NR_E = NR[ima];
if (F_E > Fmi)
{
for (j2 = 0; j2 < NP; j2++) simplex[j2, ima] = X_R[j2];
FN[ima] = F_R;
TW[ima] = TW_R;
NR[ima] = NR_R;
}
else
FN[ima] = F_E;
TW[ima] = TW_E;
NR[ima] = NR_E;
}
else
FN[ima] = F_R;
TW[ima] = TW_R;
NR[ima] = NR_R;
}
sW.WriteLine("Число итераций: " + nIt);
// Ищем лучшую вершину симплекса
int vB = -1;
minval(FN, NP + 1, ref vB);
for (i = 0; i < NP; i++) X[i] = simplex[i, vB];
}
private void buttonNelderMead_Click(object sender, EventArgs e)
{
nOfTacts = (int)numericUpDownNumberOfTacts.Value; // Число аргументов - число тактов (2, 3, 4 или 5)
double[] X = new double[nOfTacts]; // Первая вершина начального симплекса (начальная точка)
double L, L_thres, cR, alpha, beta, gamma;
int jMx = 150; // Предельное число шагов алгоритма;
int kr_todo = 50; // kr_todo - число шагов алгоритма, после выполнения которых симплекс восстанавливается
double C; // Значение критерия
turnstile = checkBoxTurnstile.Checked;
simplex = new double[nOfTacts, nOfTacts + 1]; // NP + 1 - число вершин симплекса
FN = new double[nOfTacts + 1];
TW = new double[nOfTacts + 1];
NR = new double[nOfTacts + 1];
if (nOfTacts == 2)
{
X[0] = tMinOth;
X[1] = tMinPeak;
//X[0] = 420;
//X[1] = 240;
}
else if (nOfTacts == 3)
{
X[0] = tMinOth;
X[1] = tMinPeak;
X[2] = tMinOthDay;
//X[0] = 420;
//X[1] = 240;
//X[2] = 420;
}
else if (nOfTacts == 4)
{
X[0] = tMinOth;
X[1] = tMinPeak;
X[2] = tMinOthDay;
X[3] = tMinPeak + 20;
//X[0] = 420;
//X[1] = 240;
//X[2] = 420;
//X[3] = 300;
}
else if (nOfTacts == 5)
{
X[0] = tMinOth;
X[1] = tMinPeak;
X[2] = tMinOthDay;
X[3] = tMinPeak + 20;
X[4] = tMinOth + 20;
//X[0] = 300;
//X[1] = 300;
//X[2] = 420;
//X[3] = 240;
//X[4] = 600;
}
else
{
MessageBox.Show("Плохое число тактов");
return;
}
L = 10; // Начальная длина ребра симплекса
L_thres = 0.02; // Предельное значение длины ребра симплекса
cR = 1.0; // Коэффициент отражения симплекса
alpha = 1.5; // Коэффициент растяжения симплекса
beta = 0.5; // Коэффициент сжатия симплекса
gamma = 0.5; // Коэффициент редукции симплекса
sW = new StreamWriter("_res.txt"); // Результат
sW.WriteLine("Затравка ДСЧ: " + seed);
sW.WriteLine("Параметры: ");
sW.WriteLine("Начальная длина ребра симплекса: " + L);
sW.WriteLine("Предельное значение длины ребра симплекса: " + L_thres);
sW.WriteLine("Коэффициент отражения симплекса: " + cR);
sW.WriteLine("Коэффициент растяжения симплекса: " + alpha);
sW.WriteLine("Коэффициент сжатия симплекса: " + beta);
sW.WriteLine("Коэффициент редукции симплекса: " + gamma);
sW.WriteLine("Начальная точка:");
for (int i = 0; i < nOfTacts; i++) sW.WriteLine(X[i]);
sW.WriteLine("Предельное число шагов алгоритма: " + jMx);
C = Math.Round(F(X, nOfTacts, 0)); // Значение критерия начального расписания
labelShedBest0.Text = textShed0Tact + (int)C + " (" + (int)Math.Round(TW[0]) + "+" + NR[0] + ")";
labelTimeInAll0.Text = textShed0Tact + (int)timeInAllD;
labelTimeEnd0.Text = textShed0Tact + timeLastRoutLastStop;
labelShedRoutsN.Text = textShedRoutsN + "-";
labelNCross.Text = textNCross + "-";
labelNRestruct.Text = textNRestruct + "-";
labelNViolations.Text = textNViolations + "0";
string XS_XE = "(";
foreach (double t in X) XS_XE += (int)Math.Round(t) + ", ";
XS_XE = XS_XE.Substring(0, XS_XE.Length - 2);
XS_XE += "); (";
// Поиск минимума функции Розенброка
nelMead(ref X, nOfTacts, L, L_thres, cR, alpha, beta, gamma, jMx, kr_todo);
sW.WriteLine("Результат:");
sW.WriteLine("Конечная точка:");
for (int i = 0; i < nOfTacts; i++) sW.WriteLine(X[i]);
sW.WriteLine("Значения функции в вершинах конечного симплекса:");
for (int i = 0; i < nOfTacts + 1; i++) sW.WriteLine("" + FN[i] + " = (" + TW[i] + " + " + NR[i] + ")");
sW.WriteLine("Значения времени ожидания в вершинах конечного симплекса:");
for (int i = 0; i < nOfTacts + 1; i++) sW.WriteLine(TW[i]);
sW.WriteLine("Значения числа рейсов в вершинах конечного симплекса:");
for (int i = 0; i < nOfTacts + 1; i++) sW.WriteLine(NR[i]);
sW.Close();
C = Math.Round(F(X, nOfTacts, 0)); // Значение критерия лучшего расписания
labelNPAll.Text = textNPAll + (int)nPAllD;
labelShedBestC.Text = textShedC + (int)C + " (" + (int)Math.Round(TW[0]) + "+" + NR[0] + ")";
labelTimeInAllC.Text = textShedC + (int)timeInAllD;
labelTimeEndC.Text = textShedC + timeLastRoutLastStop;
string timeSumD = "";
int tM;
foreach (double x in X)
{
tM = (int)Math.Round(x);
timeSumD += tM * nStops + "/" + tM + "; ";
}
labelTimeSum.Text = textTimeSum + timeSumD; // Суммарное время движения по маршруту без остановок, c
foreach (double t in X) XS_XE += (int)Math.Round(t) + ", ";
XS_XE = XS_XE.Substring(0, XS_XE.Length - 2); XS_XE += ")";
labelShedRoutsN.Text = "Начальные и конечные точки: " + XS_XE;
}
}
}